Summary
The main scientific objectives of C02 involve the development and verification of regularized, macroscopic, ductile damage models accounting for anisotropic material response, rate and temperature dependencies, as well as microstructural effects induced by recrystallization and phase transformation phenomena. C02 thus has a bridging function between characterization (project area B) and process technology (project area A), with the newly developed models contributing to the damage-controlled design of forming processes.
During the 2nd funding period (FP) various phenomena have been incorporated into newly developed material models that enable the simulation of advanced forming processes and enhance the prediction of material properties along the entire process chain. This includes, e.g., anisotropic plastic flow (distortional hardening) in finite elastoplasticity, which is observed to significantly influence the material response, specifically damage evolution during, e.g., shear loading. Such advanced model based prediction is most relevant for control and design of suitable load paths in metal forming, as investigated by project area A (e.g., A02, A05, A06). Before extending this distortional hardening model towards the consideration of ductile damage, a large strain gradient-enhanced anisotropic ductile damage model has been established. This fictitious (undamaged) configuration based model accounts for load path dependencies in plastic flow and damage evolution, as observed for different combinations of, e.g., tensile and shear loading sequences, and is suitable for implementation into the finite element software Abaqus. The latter is achievable since regularization of micromorphic type for plasticity and (tensorial) damage is included via two additional scalar field equations of heat equation format. A suitable Abaqus framework has been established by S01 – the Abaqus implementation of the anisotropic ductile damage model constitutes ongoing work (S01, C02). This shall make the anisotropic model available to other projects for the simulation and successful prediction of deformation induced anisotropic damage evolution in advanced metal forming including load path changes (A02, A05, A06).
Thermomechanical coupling has been investigated for steel 16MnCr5 and aluminum AW6016 (also as preliminary work for 3rd FP). Mechanical and thermal parameters are fitted – for 16MnCr5 over a wide temperature range (0 to >1200 oC). Different strain rates have been considered for 16MnCr5 with a key challenge being the appropriate incorporation of temperature dependencies in strain rate effects. As thermal softening and related localization may occur at (locally) high strain rates due to plastic heating and insufficient heat conduction, a micromorphic regularization approach of temperature contributions was implemented.
The material’s microstructure is influenced by thermomechanical processes, e.g. hot working and annealing (A02–A07). To predict its evolution and related recrystallization induced softening influencing the effective thermomechanical behavior, a physics-based large strain thermo-elastoplasticity recrystallization model was implemented. This micromechanically motivated model unifies effects of static and dynamic recovery and recrystallization, grain growth and grain refinement. It allows to predict the response of unified recrystallization for sequential loading conditions during hot working and annealing. Moreover, it enables the modeling of (initial) microstructure dependent response, specifically damage, in subsequent cold forming.
Parameters identified for the respective models are typically assumed constant for a given material, i.e. are assumed identical in and across different batches. In practice, initial material properties are associated with uncertainties due to inherent variabilities, such as variability of raw materials or production processes. Based on large strain elastoplasticity, a computationally efficient approach has been developed in collaboration with C06 (as preliminary work for 3rd FP) to quantify effects of uncertainty of homogeneously distributed material parameters on damage initiation related quantities. The model employs a numerically efficient variance-based global sensitivity analysis based on a Gaussian process regression surrogate model combined with a Bayesian active learning approach. Its application reveals variability in parameters related to nonlinear hardening response most significantly influencing damage initiation indicators. This emphasizes the potential of damage control through optimization of nonlinear hardening behavior as influenced by, e.g., heat treatment.
Heat treatment is most relevant for microstructural design, resulting material properties, and damage evolution (A02-A05, A08, A10). Towards the integrative investigation of entire process chains in the 3rd funding period, modeling of microstructural effects induced by hot working and annealing will be extended by the modeling and simulation of phase transformations (e.g., during intercritical annealing and quenching) which, subsequent to recrystallization, is a key process within the production of, e.g., DP800 steel. Damage induced by forming is intrinsically influenced by the (initial) microstructures resulting from preceding heat treatments (A02, A05). Gradient-enhanced ductile damage models shall be extended to predict the influence of (initial) microstructure resulting from phase transformations on subsequent damage evolution (implementation in cooperation with S01). Reduction of pre-existing damage can result from both, dynamic processes, such as shrinkage up to closure of voids under mechanical loads, and static processes, such as additional healing of voids under thermal input as observed in recrystallization and phase transformation processes (A04, A05, characterization by B02–B04). New damage models will include both, static and dynamic damage reduction mechanisms, enhancing the prediction of material properties along entire process chains. Uncertainty quantification of the influence of parameters on, e.g., damage evolution is a key challenge and will be investigated (with C06 based on joint preliminary work) along representative load paths. Local material properties resulting from the respective microstructure of a material may be inhomogeneously distributed. In consequence, quantification of uncertainty of related microstructural properties and parameters will be established considering their inhomogeneous distributions. This analysis contributes to the reliable simulation based prediction of process-induced properties. Further materials, such as aluminum alloys (A02, A05, A10), austenitic stainless steel (A02) and hot forming steel (A05), shall be considered in addition to DP800 and 16MnCrS5 to transfer knowledge gained and modeling frameworks established to wider applicability.
Report and current state of research
Gradient-enhanced ductile damage models
Continuum damage mechanics models are typically categorized into micromechanically motivated Gurson-type approaches, where damage evolution affects solely plastic flow through void volume fraction, and phenomenological Lemaitre-type models, where elastic material properties are additionally deteriorated by damage evolution. In C02, large strain Lemaitre-type models are developed to predict the influence of damage on material properties at macroscale (e.g., stiffness degradation). In the context of finite element simulations, local damage models may result in mesh-dependent responses together with loss of ellipticity of the governing field equations in the post-critical regime. Remedies to such mesh-dependence are the incorporation of non-local (integral) damage variables, additional gradient contributions, [Pee96], or the incorporation of viscous effects. In C02, gradient-enhanced damage models are established along the approach in [For09]. The gradient-enhanced isotropic ductile damage model developed in C02 has successfully been applied to forming processes such as air bending, [Spr20a], shape optimization, [Guh23], prediction of electrical resistance, [Güz23], and was also calibrated to DP800, [Spr20b*]. An implementation based on the framework in [Ost19] and, more recently, further improved within S01 enables the application of the gradient-enhanced ductile damage model to mesh-independent process simulation including advanced Abaqus-included features such as contact modeling. An example by analogy with forward rod extrusion processes is shown in Fig. 1a.
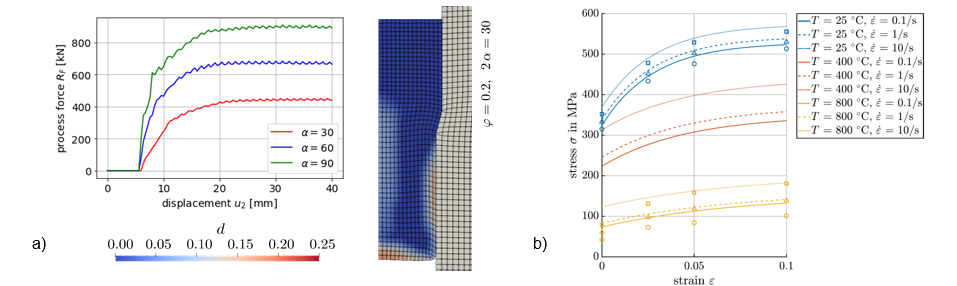 |
| Fig. 1: Grad.-enhanced ductile damage model applied to process simulation (cf. forward rod extrusion) - force-displ. re-lations for different shoulder opening angles α and distribution of damage variable d for α=60° (a). Experimental (□, △, ○) vs. simulated (lines) stress-strain data of 16MnCr5 for tensile loading at different rates and temperatures, [Opp22*] (b). |
Plastic anisotropy may strongly influence material response under, e.g., multiaxial, cyclic and shear loading, see [Kwe13] with focus on ductile damage. This anisotropy evolves due to microstructural features and different related models have been established, e.g. based on structural tensors [Kai20]. In C02, a large strain and stress-driven thermodynamically consistent distortional hardening model has been developed, [Mey21*], which guarantees yield surface convexity and includes isotropic and kinematic hardening. Experimental results for pearlitic steel are considered to assess the model’s performance revealing a significantly better fit to experimental data than previous models. Incorporation of anisotropic plasticity fundamentally contributes to the control and predictive design of load paths – and their changes – in advanced forming processes.
Prior to the combination of this hardening model – including distortional, proportional and kinematic hardening – with a ductile damage model, a large strain anisotropic ductile damage model has been developed in C02, [Spra23*]. This is based on a fictitious (undamaged) configuration and a tensorial damage metric. The model facilitates its implementation into Abaqus so that other projects, particularly of area A, can use the model for advanced metal forming simulations by analogy with the gradient-enhanced isotropic ductile damage C02 model. The originally planned route for developing a gradient-enhanced anisotropic ductile damage model, e.g. of type in [Lan20], turned out to be unsuitable for implementation into Abaqus (without user elements). This concerns the tensor-valued damage field variable within a micromorphic framework. One potential alternative would have been to introduce scalar-valued field equations related to invariants of a (symmetric second order) damage tensor, cf. [Hol22]. The new C02 model, [Spr23*], further reduces computational costs by introducing only one additional scalar-valued field equation for regularizing anisotropic tensorial damage. The same concept of a scalar damage hardening variable embedded into a micromorphic approach has been applied to anisotropic brittle damage at small strains in [Fas19]. Basis for the (future) Abaqus implementation of the new C02 model, [Spr23*], is the novel Abaqus framework established in S01, [Sob24*]. This allows incorporation of several field equations of heat equation format in addition to balance of linear momentum. Focus of the new large strain gradient-enhanced anisotropic ductile damage model, [Spr23*], was on the introduction of suitable (effective) damage driving forces and regularization of damage and plasticity. Combination of the novel model with microcrack-closure-reopening effects, [Ekh03], and kinematic hardening, [Men05], constitutes future work. The proposed fictitious configuration based model includes a damage metric bd entering the elastic Helmholtz energy Ψe(F, Fp, d(Fd)) with Fd the local incompatible damage mapping. This damage metric contributes to related invariants, i.e. Ii = I : [bd • Ee]i, and is introduced as
| (1) |
take interpretation as scalar-valued damage variables, but referred to principal damage values motivated by the load bearing area in the respective principal directions of d. Evolution of plasticity and damage are included via a two-surface model, i.e. separate initiation functions for plasticity and damage evolution, namely
| (2) |
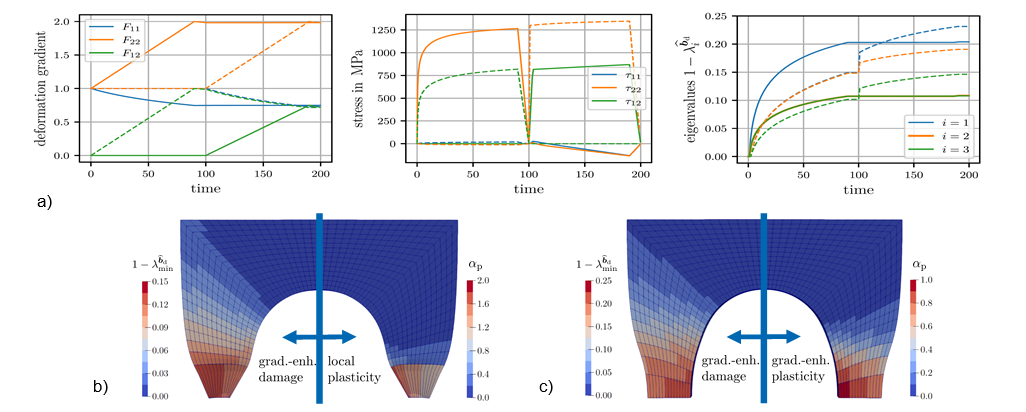
The underlying effective driving forces , d and the influence function fdp induce strong coupling between both phenomena. Effective Mandel-type stresses driving plastic flow include additional dependencies on the damage state, and damage threshold function is additionally weighted by an influence function depending on accumulated equivalent plastic strain αp. Contributions βp and βd represent nonlinear plastic and damage hardening stresses. Associated evolution equations together with Karush-Kuhn-Tucker conditions are solved monolithically at local level based on a Fischer-Burmeister algorithm – in contrast to [Guh20]. The novel model is able to predict strong load path dependencies of plastic flow and damage which may result in significantly different stress and damage states for identically deformed configurations generated along different load paths – see Fig. 2a for different tensile and shear loading sequences. This enables control of damage states, respectively prediction of improved load paths, which is of key interest for TRR 188. Moreover, a suitable set of material parameters was identified for DP800 based on data for uniaxial tension, [Spr23*].
 |
|
Fig. 2: Gradient-enhanced anisotropic ductile damage, [Spr23*]. Different combinations of tensile and shear loading sequences, as represented by coefficients of the deformation gradient, result in different Kirchhoff stresses and damage values (a); plate with hole – no sufficient regularization obtained for gradient-enhanced damage combined with local plasticity (b) but for gradient-enhanced damaged combined with gradient-enhanced plasticity (c). |
For regularization, the micromorphic framework was applied to the plasticity and damage related scalar hardening stresses βp and βd resulting in only two additional scalar field variables to be solved for. The analysis in [Spr23*] demonstrated that regularization based on these scalars is sufficient to obtain mesh-independent finite element simulation results. Regularization of the damage contribution alone, respectively of the plasticity contribution alone, is in general insufficient to regularize representative boundary value problems. Instead, regularization has to be applied to both, damage and plasticity contributions; see also [Fri23]. Fig. 2b,c show a related classic example of a plate with hole under tension for initially isotropic material and deformation induced anisotropic damage evolution. Due to symmetry, one eighth of the specimen is discretized. The respective left and right halves in Fig. 2b,c show deformed finite element meshes and contour plots of maximum damage value and accumulated equivalent plastic strain simulated based on different activation of regularization contributions. As a result, gradient-enhanced damage in combination with local plasticity does not sufficiently regularize the boundary value problem as seen by localization of the deformed mesh in Fig. 2b. To the contrary, gradient-enhancement applied to both, damage and plasticity contributions results in sufficient regularization, see Fig. 2c.
Thermomechanical coupling, recrystallization and phase transformation
During manufacturing processes, the underlying materials may undergo significant changes in temperature –either prescribed, e.g. during heat treatment, or induced by deformation. Such thermal paths at elevated temperatures influence the material response, with temperature dependent yield limits as well as microstructure evolution induced by recrystallization and phase transformations being typical related phenomena. Models have been developed in C02, also as preliminary work for the 3rd FP, that capture these phenomena and which can be combined with ductile damage models (in the 3rd FP).
A thermo-viscoplasticy model was established in C02, [Opp22*], which is applicable to ductile thermo-viscoplastic response of various materials at wide temperature ranges. As an example, its parameters are particularly verified using data for 16MnCr5. The model incorporates temperature dependent parameters of thermal, thermo-elastic, and thermo-viscoplastic type in a thermodynamically consistent manner. It covers non-linear hardening, thermal softening, heat dissipation and generation due to structural cooling and plastic deformation. The choice of functions for the temperature-dependencies, including Perzyna-type viscoplastic flow, renders the model applicable over wide temperature ranges – for 16MnCr5 it has been verified for temperature ranges from 0 to >1200 oC. The model is embedded into a thermomechanically fully coupled finite element framework so that localization, e.g. due to thermal softening under elevated mechanical loading rates, can be predicted. In case of insufficient regularization by heat conduction, the model can be combined with a micromorphic approach to regularize thermal softening effects, [Muc23]. A particular model feature is its ability to appropriately capture the influence of temperature on viscous response. This is illustrated in Fig. 1b by the comparison of experimental and simulated stress-strain relations for uniaxial tension under different loading rates and temperature levels. Its combination with gradient-enhanced damage modeling, by analogy with [Opp19] and [Fel22], constitutes future research as well as its implementation into Abaqus.
While model verification in [Opp22*] is based on experimental data generated for homogeneous strain states, model parameters for thermoplastic material response are identified on the basis of full field data in [Ros21*]. Aluminum alloy AW6016 was elaborated, as also relevant for the 3rd FP, with the focus on small changes in temperature induced by deformation under tensile loading. Full field digital image correlation data and full field thermography data were used for the purpose of parameter identification in the framework of the Finite-Element-Model-Updating (FEMU) method. The thermo-elastoplasticity model demonstrates identifiability of the model parameters for the experimental data considered. A key aspect of the model [Ros21*] is the application of an additional non-standard contribution to the Helmholtz energy in the form of
| (3) |
Therein, the additional model parameter υ controls the amount of dissipation resulting from plastic deformation and contributing to the heat source. In contrast to other well-established approaches, such as the introduction of a Taylor-Quinney factor, the proposed formulation aims at thermodynamically consistent scaling of dissipation. For the experiments considered in [Ros21*], the model shows excellent agreement between measured and simulated temperature fields. The parameter identification framework can be transferred to other materials and suitable experiments. Further applications of the FEMU approach for time dependent material response in combination with gradient-enhanced damage are elaborated in [Sch20*]. Suitable starting values for parameter identification within FEMU can be generated via the neural network (NN) framework proposed in [Sch23*] which considers homogeneous deformation states. The NN was trained by different model parameter sets and for different combinations of mechanical loading paths, making it directly applicable to experimental data at different temperature levels.
A physics-based micromechanically motivated large strain thermo-elastoplasticity recrystallization model unifying effects of static and dynamic recovery, static and dynamic recrystallization, grain growth and grain refinement – as present in processes such as hot forming and heat treatment – was implemented, [Böd23b*], to predict microstructure evolution and related recrystallization dependent softening affecting the effective thermomechanical behavior. The hypo-elasticity based recrystallization model in [Cho19] was transferred to a hyper-elasticity based thermo-elastoplasticity model to overcome limitations inherent to hypo-elasticity based approaches. The model and its implementation are a key basis for developments in the 3rd FP and shall be combined with modeling of (initial) microstructure dependent damage evolution in (subsequent) cold forming. An alternative back-stress related approach is investigated in [Moh22]. In its present form, the C02 model includes temperature dependent Hencky-type hyper-elasticity combined with non-associative temperature dependent hardening minus recovery for variable αp in Armstrong-Frederick format,
| (4) |
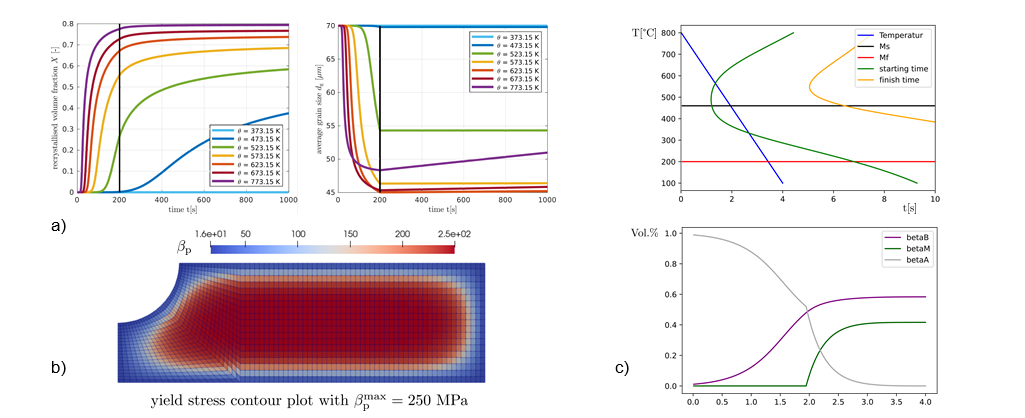
with absolute temperature θ, plastic multiplier λp and hardening stress βp. The recovery activation functions Rd,s are of Arrhenius type. Physically motivated evolution equations are introduced for the increase and decrease of recrystallized volume fraction X as well as of average grain size dg. The proposed model results in a thermodynamical consistency condition that constrains the evolution of X and dg and gives rise to the thermodynamic relation between these. The model’s capability to predict the material response for thermomechanical sequential loading is demonstrated in Fig. 3a,b. This simulation involves a first hot working step, enforcing homogeneous states under uniaxial tension, followed by unloading and holding at various temperatures in a second step, Fig. 3a. The results show a sigmoidal evolution of recrystallized volume fraction and grain size reduction followed by grain size growth amongst other phenomena. The model was embedded in a thermomechanically fully coupled finite element formulation. Fig. 3b shows related simulation results where, due to inhomogeneous temperature distribution and static recrystallization, the yield limit near the boundary is reduced in contrast to inner regions of the specimen. It enables the prediction of (initial) microstructure dependent material response, specifically damage, in (subsequent) cold forming.
In view of the key importance of phase transformation phenomena occurring during, e.g., intercritical annealing (as considered in A04) and quenching (A05), preliminary work on the formulation of suitable related models has been implemented which, moreover, constitutes ongoing research work, particularly with regard to its finite element implementation into Abaqus. At this stage, the formation of martensite by non-diffusive phase transformation is covered by a purely temperature dependent Koistinen-Marburger model, i.e.
| (5) |
with martensite and austenite volume fractions ξM and ξA, martensitic start temperature MS, and transformation rate k. Additional diffusive phase transformation, such as formation of bainite, is modeled with an isothermal Johnson-Mehl-Avrami-Kolmogorov relation, [deO13]. An exemplary cooling path (TTT diagram) and related simulation based prediction of phase volume fraction evolutions is highlighted in Fig. 3c. Further developments shall account for respective mechanical contributions within a homogenization, respectively mixture approach, see [Bar21] and with focus on plasticity related contributions see [And22]. This enables the prediction of (initial) microstructure dependent material response in (subsequent) cold forming.
 |
|
Fig. 3: Finite thermoplasticity with static and dynamic recovery, static and dynamic recrystallization, grain growth and grain refinement (a-b) [Böd23b*] – response (recrystallized volume fraction, grain size) under uniaxial tension, unloading and holding at different temperatures (a) and FE simulation of static recrystallization (b); exemplary cooling path (TTT diagram, martensite finish temperature Mf) and simulation of phase volume fractions for austenite, martensite, bainite (c). |
Uncertainty quantification
Consideration of uncertainties was originally planned for the 3rd FP. Due to the shift from C05 to C06 within the 3rd FP and related changes in scientific methods, joint preliminary work (C02, C06) focused on uncertainty quantification, [Böd23a*]. This research particularly elaborates on the effect of uncertainty of homogeneously distributed parameters on extremal values of interest, such as stress triaxiality and Lode angle in plastically deformed devices, since these are accepted as key indicators for damage initiation in metal forming. The effects of material parameter uncertainty on stress triaxiality and Lode angle are quantified by means of a numerically efficient variance-based global sensitivity analysis framework together with a Gaussian process regression surrogate model and is combined with Bayesian active learning. This sensitivity analysis, in form of Sobol’ sensitivity indices Si, is based on expected value EΘ and variance VΘ, i.e.
| (6) |
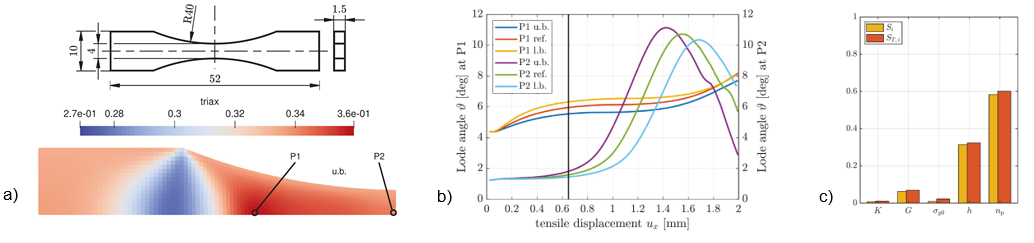
wherein θ corresponds to a set of material parameters realized by random variables Θ with Θ-i corresponding to Θ without Θi. Moreover, y = 𝑔(θ) is a maximum value of interest, such as maximum stress triaxiality within the considered domain. Fig. 4 shows results of the established formulation by the analysis of a notched specimen under tension. Due to symmetry and homogeneously distributed material parameters, one eighth of the specimen is considered within the underlying finite element simulations. Fig. 4a shows the distribution of stress triaxiality at a particular loading stage (prior to necking), whereas Fig. 4b shows the evolution of stress triaxiality at two representative positions for different material parameter sets. As a key result of the uncertainty quantification, main and total Sobol’ sensitivity indices Si and ST,i for maximum stress triaxiality as established damage initiation indicator show particularly high sensitivity for parameters related to nonlinear hardening, Fig. 4c. The results underline the potential of damage control through optimization of the material’s nonlinear hardening behavior influenced by, e.g., heat treatment. In particular, to ensure accurate predictions of damage, special emphasis must be placed on the fitting of material parameters describing the nonlinearity of the hardening response. This preliminary work contributes to reliable simulation based prediction of process-induced properties and is most useful for its extension towards, e.g., more advanced material models and the consideration of inhomogeneous distributions of model parameters.
 |
|
Fig. 4: Notched specimen and stress triaxiality distribution at a load state prior to necking generated by FE simulation of one eighth of the specimen (a); stress triaxiality evolut. at points P1 and P2 for different mat. parameter sets (b); main and total Sobol’ sensitivity indices Si and ST,i of the underlying parameters associated with maximum stress triaxiality (c). |
Conclusions
During the 2nd FP, gradient-enhanced ductile damage models were extended – in particular to anisotropic ductile damage suitable for implementation into Abaqus and including gradient-enhancement of plasticity related contributions. This enabled the successful use and application of the models for mesh-independent forming process simulations by analogy with the previously established and verified gradient-enhanced isotropic damage model successfully applied to, e.g., air bending, extrusion processes, and prediction of electrical resistance in a formed specimen. This anisotropic formulation had to follow a different derivation and implementation (suitable for Abaqus) than originally planned. While further model extensions, such as anisotropic distortional hardening, thermal softening and rate-dependent effects over wide temperature ranges, have been established in the 2nd FP, their combination with gradient-enhanced ductile damage still constitutes future research. Instead, in a collaborative work together with new project C06 and as preliminary work for the 3rd FP, a computationally efficient framework for uncertainty quantification was established. In addition to preliminary work on phase transformations, a finite thermoplasticity model for static and dynamic recovery and recrystallization, grain growth and grain refinement was developed and implemented for thermomechanically fully coupled finite element simulations. This enables the prediction of recrystallization dependent softening effects, microstructure evolution and related effects on (subsequent) cold forming processes.
Further challenges in the area of macroscopic modeling of damage in forming processes concern the transition of established models to the simulation of other materials. This may require further model extensions in addition to verification. Additional phenomena such as thermomechanically induced reduction of (pre-existing) damage is not comprehensively included in the current state of research, which similarly applies to more advanced uncertainty quantification analysis. Interactions of recrystallization and phase transformation phenomena, which trigger particular microstructures of the respective metals, with damage evolution are, at this stage, neither fully understood nor sufficiently predictable by advanced modeling and simulation.
Project- and subject-related list of publications
| [Alf04] | K.S. Alfredsson, U. Stigh (2004) Continuum damage mechanics revised – A principle for mechani-cal and thermal equivalence. Int. J. Solids Struct., 41:4025-4045, DOI:10.1016/j.ijsolstr.2004.02.052 |
| [And22] | Andersson, B., Ahlström, J., Ekh, M., Josefson, B.L. (2022) Homogenization based macroscopic model of phase transformations and cyclic plasticity in pearlitic steel. J. Therm. Stress., 45(6):470-492, DOI:10.1080/01495739.2022.2056557 |
| [Ban10] | Banabic, D. (2010) Sheet Metal Forming Processes. Springer, DOI:10.1007/978-3-540-88113-1 |
| [Bar21] | Bartel, T., Geuken, G.-L., Menzel, A. (2021) A thermodynamically consistent modelling framework for strongly time-dependent bainitic phase transitions. Int. J. Solids Struct., 232:111172, DOI:10.1016/j.ijsolstr.2021.111172 |
| [Böd23a*] | Böddecker, M., Faes, M.G.R., Menzel, A., Valdebenito, M.A. (2023) Effect of uncertainty of ma-terial parameters on stress triaxiality and Lode angle in finite elasto-plasticity – a variance-based global sensitivity analysis. Adv. Ind. Manuf. Eng., 7:100128, DOI:10.1016/j.aime.2023.100128 |
| [Böd23b*] | Böddecker, M., Menzel, A. (2023) A large strain thermoplasticity model including recovery, re-crystallisation and grain size effects. Proc. Appl. Math. Mech., 23(4):e202300282, DOI:10.1002/pamm.202300282 |
| [Cho19] |
Cho, H.E., Hammi, Y., Bowman, A.L., Karato, S., Baumgardner, J.R., Horstemeyer, M.F. (2019) A unified static and dynamic recrystallization Internal State Variable (ISV) constitutive model coupled with grain size evolution for metals and mineral aggregates. Int. J. Plast., 112:123-157, DOI:10.1016/j.ijplas.2018.08.009 |
| [deO13] | de Oliveira, W.P., Savi, M.A., Pacheco, P.M.C.L. (2013) Finite element method applied to the quenching of steel cylinders using a multi-phase constitutive model. Arch. Appl. Mech., 83:1013-1037, DOI:10.1007/s00419-013-0733-x |
| [Ekh03] | Ekh, M., Menzel, A., Runesson, R., Steinmann, P. (2003) Anisotropic damage with the MCR effect coupled to plasticity. Int. J. Eng. Sci., 41(13-14):1535-1551, DOI:10.1016/S0020-7225(03)00032-6 |
| [Fas19] | Fassin, M., Eggersmann, R., Wulfinghoff, S., Reese, S. (2019) Gradient-extended anisotropic brittle damage modeling using a second order damage tensor – theory, implementation and nu-merical examples. Int. J. Solids Struct., 167:93-126, DOI:10.1016/j.ijsolstr.2019.02.009 |
| [Fel22] | Felder, S., Kopic-Osmanovic, N., Holthusen, H., Brepols, T., Reese, S. (2022) Thermo-mechanically coupled gradient-extended damage-plasticity modeling of metallic materials at finite strains. Int. J. Plast., 148:103142, DOI:10.1016/j.ijplas.2021.103142 |
| [For09] | Forest, S. (2009) Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J. Eng. Mech., 135(3):117-131, DOI:10.1061/(ASCE)0733-9399(2009)135:3(117) |
| [Fri23] |
Friedlein, J., Mergheim, J., Steinmann, P. (2023) Efficient gradient enhancements for plasticity with ductile damage in the logarithmic strain space. Euro. J. Mech. A/Solids, 99:104946, DOI:10.1016/j.euromechsol.2023.104946 |
| [Fae21] | Faes, M.G., Daub, M., Marelli, S., Patelli, E., Beer, M. (2021) Engineering analysis with probability boxes: A review on computational methods. Struct. Saf., 93:102092, DOI:10.1016/j.strusafe.2021.102092. |
| [Guh20] | Guhr, F., Sprave, L., Barthold, F.-J., Menzel, A. (2020) Computational shape optimisation for a gradient-enhanced continuum damage model. Comp. Mech., 65:1105-1124, DOI:10.1007/s00466-019-01810-3 |
| [Guh23] | Guhr, F., Barthold, F.-J. (2023) Variational sensitivity analysis and shape optimisation applied to a non-local ductile damage model. Comp. Mech., DOI:10.1007/s00466-023-002377-w |
| [Güz23] | Güzel, D., Kaiser, T., Lücker, L., Baak, N., Walther, F., Menzel, A. (2023) Characterisation of dam-age by means of electrical measurements: numerical predictions. Proc. Appl. Math. Mech., 23(2):e202300013, DOI:10.1002/pamm.202300013 |
| [Hol22] | Holthusen, H., Brepols, T., Reese, S., Simon, J.-W. (2022) A two-surface gradient-extended aniso-tropic damage model using a second order damage tensor coupled to additive plasticity in the logarithmic strain space. J. Mech. Phys. Solids, 163:104833, DOI:10.1016/j.jmps.2022.104833 |
| [Kai20] | Kaiser, T., Lu, J., Menzel, A., Papadopoulos, P. A covariant formulation of finite plasticity with plasticity-induced evolution of anisotropy: modeling, algorithmics, simulation, and comparison to experiments. Int. J. Solids Struct., 185-186:116-142, DOI:10.1016/j.ijsolstr.2019.08.005 |
| [Kou08] | Kouznetsova, V., Geers, M.G.D. (2008). A multi-scale model of martensitic transformation plastici-ty. Mech. Mat., 40:641-657, DOI:10.1016/j.mechmat.2008.02.004 |
| [Kwe13] | Kweon, S. (2013) Investigation of shear damage considering the evolution of anisotropy. J. Mech. Phys. Solids, 61(12):2605-2624, DOI:10.1016/j.jmps.2013.08.006 |
| [Lan20] | Langenfeld, K., Mosler, J. (2020) A micromorphic approach for grad.-enhanced anisotropic ductile damage. Comp. Methods Appl. Mech. Engrg., 360:112717, DOI:10.1016/j.cma.2019.112717 |
| [Men05] | Menzel, A., Ekh, M., Runesson, K., Steinmann, P. (2005) A framework for multiplicative elastoplas-ticity with kinematic hardening coupled to anisotropic damage. Int. J. Plast., 21(3):397-434, DOI:10.1016/j.ijplas.2003.12.006 |
| [Mey21*] | Meyer, K.A., Menzel, A. (2021) A distortional hardening model for finite plasticity. Int. J. Solids Struct., 232:111055, DOI:10.1016/j.ijsolstr.2021.111055 |
| [Moh22] | Mohammadpour, A., Geers, M.G.D., Kouznetsova, V.G. (2022) Multi‑scale modeling of the thermo‑mec. behavior of cast iron. Multiscale Sci. Eng., 4:119-136, DOI:10.1007/s42493-022-00081-0 |
| [Muc23] | Mucha, M., Rose, L., Wicislo, B., Menzel, A., Pamin, J. (2023) Experiments and numerical simula-tion of Lueders bands and Portevin-Le Chatelier effect in aluminium alloy AW5083. Arch. Mech., 75(3):301-336, DOI:10.24423/aom.4204 |
| [Nol20] | Noll, I., Bartel, T., Menzel, A. (2020) A computational phase transformation model for selective laser melting processes. Comp. Mech., 66:1321-1342, DOI:10.1007/s00466-020-01903-4 |
| [Opp19] | Oppermann, P., Denzer, R., Menzel, A. (2019) Finite-strain thermo-viscoplasticity for case-hardening steels over a wide temperature range. Proc. Appl. Math. Mech., 19:e201900237, DOI:10.1002/pamm.201900237 |
| [Opp22*] | Oppermann, P., Denzer, R, Menzel, A. (2022) A thermo-viscoplasticity model for metals over wide temperature ranges – application to case hardening steel. Comp. Mech., 69:541-56, DOI:10.1007/s00466-021-02103-4 |
| [Ost19] | Ostwald, R., Kuhl, E., Menzel, A. (2019) On the implementation of finite deformation gradient-enhanced damage models. Comp. Mech., 64(3):847-877, DOI:10.1007/s00466-019-01684-5 |
| [Pee96] | Peerlings, R.H.J., de Borst, R., Brekelmans, W.A.M., de Vree, J.H.P., Spee, I. (1996) Some ob-servations on localisation in non-local and gradient damage models, Euro. J. Mech. A/Solids, 15:937-953, https://research.tue.nl/en/publications/2b303112-d927-488a-ad1b-46669e5e28bb |
| [Ros21*] |
Rose, L., Menzel, A. (2021) Identification of thermal material parameters for thermo-mechanically coupled material models. Meccanica, 56:393-416, DOI:10.1007/s11012-020-01267-2 |
| [Sch20*] | Schulte, R., Ostwald, R., Menzel, A. (2020) Gradient-enhanced modelling of damage for rate-dependent material behaviour – a parameter identification framework. Materials, 13(14):3156, DOI:10.3390/ma13143156 |
| [Sch23*] | Schulte, R., Karca, C., Ostwald, R., Menzel, A. (2023) Machine learning-assisted parameter identi-fication for constitutive models based on concatenated loading path sequences. Euro. J. Mech. A/Solids, 98:104854, DOI:10.1016/j.euromechsol.2022.104854 |
| [Sob24*] | Sobisch, L., Kaiser, T., Furlan, T., Menzel, A. (2024) A user material approach for the solution of multi-field problems in Abaqus: Theoretical foundations, gradient-enhanced damage mechanics and thermo-mech. coupling. Finite Elem. Anal. Des., 232:104105, DOI:10.1016/j.finel.2023.104105 |
| [Son22] | Song, J., Wei, P., Valdebenito, M.A., Faes, M., Beer, M. (2022) Data-driven and active learning of variance-based sensitivity indices with Bayesian probabilistic integration. Mech. Syst. Signal Pro-cess., 163:108106, DOI:10.1016/j.ymssp.2021.108106 |
| [Spr20a] | Sprave, L., Schowtjak, A., Meya, R., Clausmeyer, T., Tekkaya, A.E., Menzel, A. (2020) On mesh dependencies in finite-element-based damage prediction: Application to sheet metal bending. Prod. Eng., 14:123-134, DOI:10.1007/s11740-019-00937-9 |
| [Spr20b*] | Sprave, L., Menzel, A. (2020) A large strain gradient-enhanced ductile damage model – Finite element formulation, experiment and parameter identification. Acta Mech., 231(12):5159-5192, DOI:10.1007/s00707-020-02786-5 |
| [Spr23*] | Sprave, L., Menzel, A. (2023) A large strain anisotropic ductile damage model – Effective driving forces and gradient-enhancement of damage vs. plasticity. Comp. Methods Appl. Mech. Engrg., 416:116284, DOI:10.1016/j.cma.2023.116284 |
| [Voy11] | Voyiadjis, G.Z., Shojaei, A., Li, G., Kattan, P.I. (2011) A theory of anisotropic healing and damage mechanics of materials. Proc. R. Soc. A, 468:163-183, DOI:10.1098/rspa.2011.0326 |
| [Yad12] | Yadegari, S.Turteltaub, S., Suiker, A.S.J. (2012) Coupled thermomechanical analysis of transfor-mation-induced plasticity in multiphase steels. Mech. Mat., 53:1-14, DOI:10.1016/j.mechmat.2012.05.002 |