Summary
The objective of project C05 within the second funding period was the extended research of controlling damage by applying the concept of numerical optimization. This was achieved in multiple disciplines. First, academic problems were researched by applying a variational sensitivity analysis. Second, an optimization strategy using the software Abaqus was developed to consider industrial problems within TRR188.
The variational sensitivity analysis was applied to the model developed by project C02 within the first funding period. This enabled consideration of ductile damage material behavior within the optimization. The gathered results from academic-like problems allowed making generalized conclusions regarding damage optimization.
Since the modelling of complex forming processes in project area A requires robust and efficient implementations of contact mechanics, an optimization framework around the commercial software Abaqus was developed. This can take existing models into account and, with parametrization and python scripts, allows the arbitrary optimization of these forming processes.
Finally, project C05 provided gradient information and code for geometric optimization to the new project C06, to support their research for the upcoming third funding period.
Report and current state of research
Variational sensitivity analysis
In the first funding period, the concept of variational sensitivity analysis was applied to a regularized damage model, developed in cooperation with project C02, allowing numerical optimization of damage [*Guh20]. In parallel, project C02 developed a regularized ductile damage model [Spr20]. This model can accurately describe the behavior of the material utilized in processes of TRR188. Based on these two results, the concept of variational sensitivity analysis from [*Guh20] was applied to the gradient-extended, non-local ductile damage model developed by project C02 [Spr20], to enable numerical optimization.
To compute the gradients of the employed model and to allow their utilization in the optimization, a variational sensitivity analysis δw = -K-1 was applied. This equation describes how a change in the design variables s leads to a change in the field variables w = [u, Φ] i.e. displacement u and non-local damage Φ. The choice of the design variables s finally defines the underlying optimization problem. However, due to the inclusion of plastic effects, as well as a local damage formulation, history dependencies had to be taken into account. This was captured with the history sensitivity matrix H = r / hn and the total variation of the history field Zn = h / hn, where r denotes the global residual, h the history field from the current and hn from the previous loadstep. While the history sensitivity matrix was calculated in a straight forward manner like the pseudo load matrix P = r / s, the total variation of the history field had to be updated iteratively after each converged global Newton step of the finite element simulation [*Guh21b]. With this inclusion of history dependence, an adaptation to the standard optimization framework was required [*Lie20].
The resulting gradients were employed in shape optimization by specifying the design variables as the referential geometric description, i.e. s = X, where X denotes the matrix of all nodal coordinates. The first two optimization problems aimed to directly minimize the accumulated damage within the body. This was captured with the squared norm of the nodal damage vector of the non-local damage quantity, i.e. ||Φ(s)||².
Two different optimization problems were stated, i.e. an unconstrained, see Eq. (1), and a damage constrained, see Eq. (2). In the second problem, the nodal damage quantities were additionally constrained by a critical damage value . The chosen problem was the academic plate with a hole for its simple geometry leading to an inhomogeneous stress state. The specimen was loaded at the top and bottom with a prescribed displacement. Application of symmetry conditions allowed reduction of the simulated geometry requiring only one eighth of the complete geometry. The material parameters for the simulations were taken from parameter identifications made by C02 for DP800 steel [Spr20]. The two optimization problems read
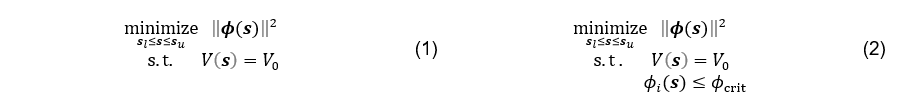
To allow direct comparison, both optimization problems were subjected to a volume constraint . Hereby denotes the initial volume of the referential plate design. The results from these optimizations are depicted in Fig. 1. In the presented result for the damage constrained optimization, an arbitrary critical value was chosen to limit the maximal damage attainable at each finite element node, i.e. Φi(s).
 |
|
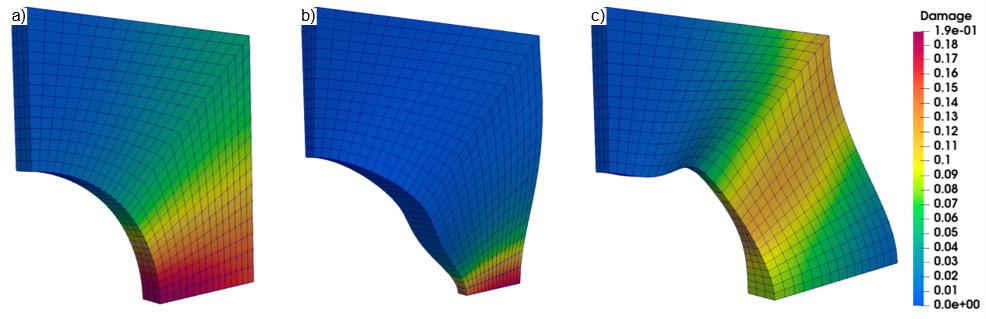
Fig. 1.: Shape optimization of two damage optimization problems. a) The reference geometry, b) the unconstrained optimization and c) the constrained optimization. The shapes depict the undeformed geometry, with the damage distribution resulting from the applied load. |
The optimization without the added damage constraint (1) yielded an undesirable geometrically induced early localization of damage. The optimizer reduced the lower cross-section, which restricted the damage evolution to occur only in this small area. While this solution reduced the overall damage accumulation by 66%, it did not reduce the maximal damage value. An addition of nodal damage constraints in optimization problem (2) circumvented the previously described behavior. The overall damage accumulation in this problem was reduced by spreading out the overall damage evenly throughout the body [*Guh23a].
The addition of these nodal constraints Φi(s), however, came with a cost in computation and optimization time, since the optimizer had to consider the new restrictions in design space. In addition, the overall reduction in accumulated damage could only be reduced by 40% in this problem. However, the constrained solutions with lower critical damage values showed a better damage resistant behavior, detectable in their respective load-displacement curves. While the damage evolution in the reference plate, as well as the unconstrained plate, started to localize, this behavior was not detectable in the constrained problem. This indicated, that these types of structures can withstand higher deformations before critical damage localization starts to occur.
Concluding these results, it is possible to extrapolate them to general optimization problems regarding damage. Consequently, one has to keep in mind that simply minimizing the damage accumulation in a given body may lead to unsatisfying results like early damage localization. This can be circumvented by including additional damage constraints.
The second type of optimization aimed to analyze, whether the additional effort of employing such complex damage material models, i.e. the C02 model, within an optimization is beneficial. For this purpose, the compliance C(s) was chosen, as this objective can be defined independently of the underlying material model. Minimization of this quantity led to an increased stiffness of the optimized shape. As this quantity was only directly dependent on the elastic energy contributions, a change of the material parameters to switch between purely elastic, elasto-plastic and completely coupled behavior, respectively, allowed direct comparison of different material behaviors.
 |
|
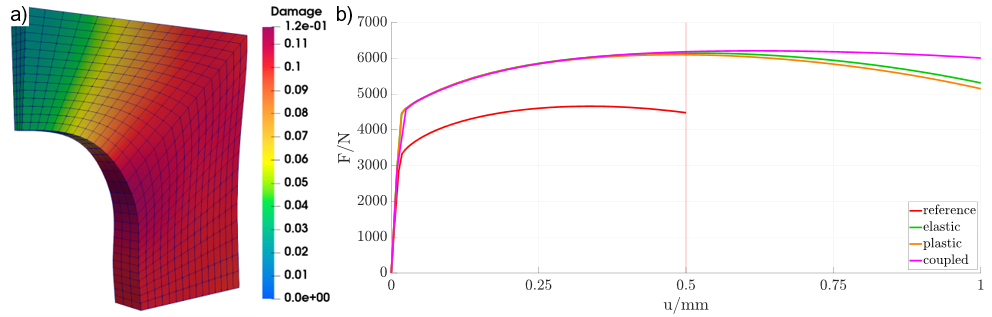
Fig. 2.: a) The design resulting from the coupled optimization in its undeformed shape with the damage distribution resulting from the applied load. b) The load-displacement curves of the three optimal designs. The vertical dashed red line indicates the maximum load applied within the optimization. |
To disable the damage or plastic behavior, certain material parameters which govern the onset of plastic and damage evolution, respectively, had to be increased significantly. With this, it was possible to compare different material behaviors using the same material model. The optimization problem for each of these subproblems read the same, i.e.

Therein, a volume constraint was added again, to ensure that the same amount of material was utilized. As such, the resulting designs could be compared directly.
The respective results of the elastic, elasto-plastic and coupled results are summarized in Table 1. While the unadjusted results varied greatly in their value, the computed adjusted results, i.e. the elastic and elasto-plastic geometries were retroactively simulated with the completely coupled C02 model, did not show a significant variance in the optimized objective, contrary to what would have been expected. While the coupled result still yielded the overall lowest value, the elastic and elasto-plastic shapes only differed by 2.1% and 3.25% from the overall optimum, respectively. This was also detectable in the load-displacement curves in Fig. 2. Therein, the point at which the optimization was conducted is indicated by the vertical dashed red line, i.e. at mm. Similar to the objective values, the three values at u = 0.5 mm only varied slightly by approximately 40-80 N, suggesting no immediate benefit of running optimizations with more complex material models.
However, a closer look at the curvature at these points indicated general distinctive behavior between the different set of curves. While the elastic and elasto-plastic curves seemed to have reached their peak of applicable force, the curve of the coupled problem still showed a positive inclination. This prompted further analysis by additional loading of the shapes up to u = 1.0 mm [*Guh23b]. This further loading showed that the coupled solution did in fact show a more damage tolerant behavior. The elastic and elasto-plastic shapes started to significantly lose their stiffness properties due to accumulation of damage, while the coupled solution showed an inherent resistance to damage accumulation.
Concluding, an extrapolation of these results indicates that it is worthwhile to compute actual damage mechanics when running simulations taking damage into account. While the stress-triaxiality η = σn / σvM is still widely used to predict damage behavior and analyze processes, damage simulations and their application within optimization can yield better results, even if not directly noticeable at a first glance.
It was initially planned to extend the employed material model used within the optimization to include temperature and viscous effects. But its application within the variational approach was abandoned. The application of temperature and time dependent effects, was instead shifted to the optimization framework utilizing the commercial software Abaqus. On the one hand, the significantly high computation cost was a concern. The implementation of variationally derived sensitivities, compared to simple numerically computed gradients, is very efficient. However, the underlying complexity of the additional material effects together with its implementation within Matlab lead to high computation times, which significantly increase with the additional optimization routine. On the other hand, the temperature effects for example are of main concern in actual forming processes, e.g. rod extrusion, wherein the contact mechanics cannot be omitted. Therefore, the focus while applying the concept of variational sensitivity analysis was placed on the C02 model and gathering results from academic examples, which can be transferred conceptually to problems of larger scope.
Optimization utilizing commercial software
Within the first funding period, an optimization framework around the commercial software Abaqus, widely used within TRR188, together with elements from Python and Matlab was developed to enable direct numerical optimization of the researched forming processes. This development was necessary, because application of any variational sensitivity analysis would have required (i) the handling of contact mechanics within the finite element environment and (ii) the nontrivial derivation of the gradients. The initial implementation was based on changing the easy-to-read text data within the input-files (.inp) of the underlying forming process. With this it was able to optimize simple problems for air bending, concerning external loads, amplitudes and simple geometries, cf. [*Guh19a,*Guh19b,*Guh21a]. However, this approach was rather limited when aiming to optimize more complex processes, as they have to be remodeled outside of the Abaqus environment. Consequently, certain mappings between the two systems, i.e. Abaqus simulation and Matlab optimization, are required, which has significant drawbacks when optimizing complex geometries.
The method developed in the second funding period aims to utilize already existing simulation model available at the institutes. By altering data stored in these model data bases (.cae), it was possible to create new simulations files at each iteration step within the optimization. These got created by Abaqus directly, circumventing the mapping, and did not require the creation of lengthy python scripts. However, this method required small adaptations within the model data bases to enable optimization, as the design variables of the optimization had to be made identifiable and changeable within the model data bases, e.g. geometric parameters needed to be parametrized such that a change in their value changed the underlying geometry accordingly.
Matlab was again used as the software which controlled all underlying software and ran the simulations. Abaqus was used to generate new simulation models which were calculated afterwards. Python was used to adjust the changes for the data bases and extracted the data after the completed simulation, which was used within the Matlab optimization. After a successful optimization, the simulation data was additionally stored in .vtk-files for post-processing purposes.
The optimizations could be run with gradient-based, as well as gradient-free methods, wherein the latter had proven to be more applicable for the contact problems analyzed within TRR188. The numerical gradients evaluated for the gradient-based method could yield unsatisfactory search directions, which might yield worse optimal solutions or, in worst cases, no convergence at all. This was already observed in later problems within the first funding period. Since the optimization with gradient-free methods, combined with the lengthy simulation times of the processes analyzed within TRR188, took a lot of computation time, an additional constraint check was introduced within the framework. As many of the underlying process parameters analyzed were of geometric type and certain constraints were dependent on these parameters, the constraints could be checked without running the expensive finite element simulations.
One of the main challenges of this framework within the second funding period was the concern of simulation time. Since many projects from project area A within TRR188 extended the scope of their research, this led to many of the processes requiring long simulation times for single simulations. Consequently, additional optimization of these processes was difficult to handle in a timely manner, which prompted the application of this framework to be limited to 2d simulations, as these could still require weeks of computation time to converge.
Concluding, a framework was developed which allows direct optimization of the damage behavior in industrial forming processes. The framework is integrated closely to already existing simulations and thereby allows easy incorporation of new and existing forming problems. The proposed framework was made available to TRR188 for its utilization within the third funding period.
Optimization with commercial software: rod extrusion
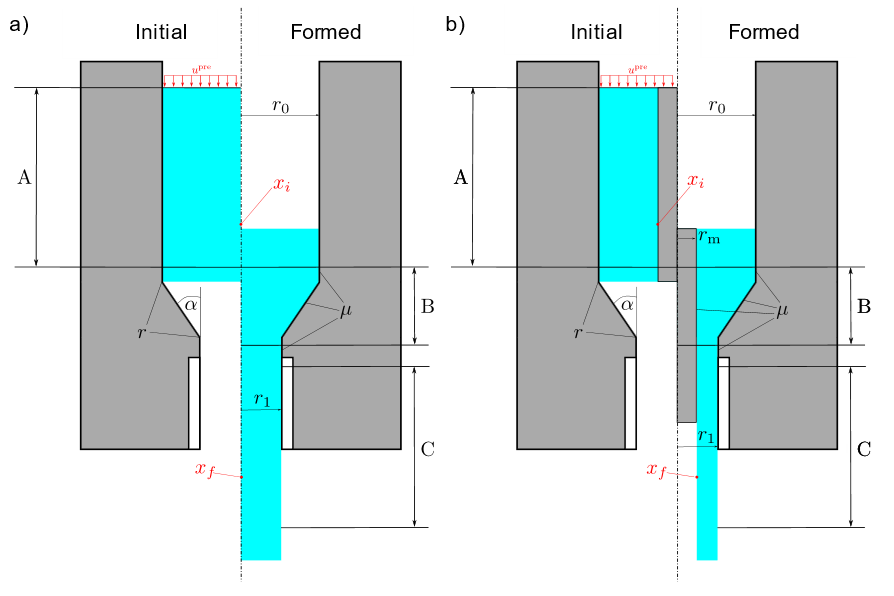
The initial application for the framework described above was in cooperation with project A02 in the field of rod extrusion processes. Initially, the optimization framework was validated, to ensure that it yielded sufficient results by comparing the numerically optimized results to the results obtained from project A02 in the first funding period for the process of full forward rod extrusion [Her20]. The model was taken from previous work made by project A02 and parametrized to enable the optimization procedure. The objective function was chosen to be the mean triaxiality ηmean [Her20,*Guh23c] of a single element on the center axis of the billet. Its development was only analyzed during plastic deformation. To ensure correct evaluation, the analyzed element had first to start in the elastic area, completely transverse through the plastic deformation zone and finally end up in the steady-state area of the forming process. This is depicted in Fig. 3 together with the process of forward hollow extrusion.
The results from the optimization for the most important process parameters, i.e. the extrusion strain εex and shoulder opening angle 2α, showed very good accordance with the results gathered by project A02 within the first funding period. These parameters had the highest influence on the process when considering damage evolution, and as such they saw the biggest and most immediate changes throughout the optimization. Additionally, their values reached the desired values of a high extrusion strain and a low shoulder opening angle. Similarly, the friction parameter showed a smaller influence within the optimization. However, the results for the transition radius did not coincide with the results from project A02. With its low impact on damage within the process overall however, this validation was deemed successful and consequently applied to other processes.
 |
|
Fig. 3.: a) The process of full forward extrusion and b) forward hollow extrusion. Each image represents the initial configuration on the left and the formed one on the right. Indicated are elastic (A), plastic deformation (B) and steady-state zone (C). The indicate the approximate position of the evaluated element initially (i) and finally (f). |
The optimization was extended to the extrusion process of forward hollow extrusion, see Fig. 3. This process introduced a mandrel with radius rm into the center of the workpiece, to create hollow work-pieces. The process was analyzed in two steps with two separate optimization problems. Both problems used the same objective function ηmean as in the full forward rod extrusion optimization. The first optimization aimed to verify, if similar conclusions like in full forward rod extrusion regarding the behavior of extrusion strain and shoulder opening angle could be drawn, which were both chosen as design variables for the optimization. The results indicated the same behavior, i.e. the extrusion strain got maximized, while the shoulder angle got minimized. In the second optimization, instead of the extrusion strain, the final r1 and mandrel radius rm were the design variables. This required the additional constraint regarding the extrusion strain, limiting its upper and lower bounds.
Since the extrusion strain is a function of the three radii, i.e. εex =(r0, r1,rm) with r0 held constant, its value was now dependent on two design variables. The expected outcome of the optimization was that the extrusion strain would again be maximized, with one of the radii reaching their restrictive upper or lower bound. While the former was again confirmed, quite interestingly, neither of the optimal radii values reached their respective bounds. Instead, the optimal solution lay in the middle of the design space, indicating that this process has an optimal combination of die and mandrel with respect to the damage evolution [*Guhr23c].
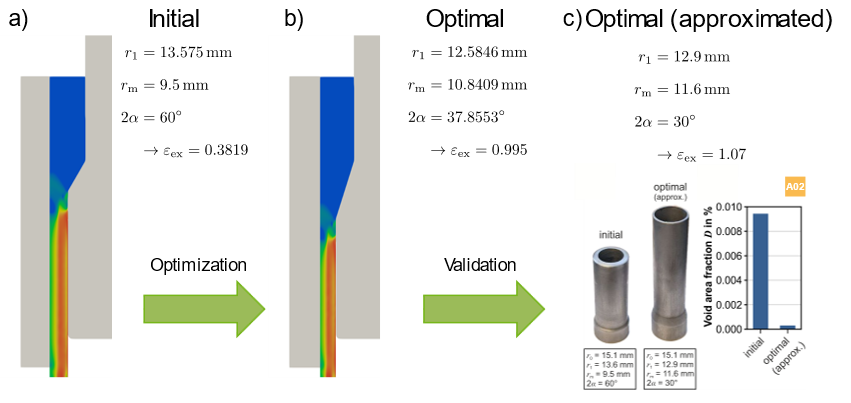
Finally, the optimization results were validated. This required an additional set of optimizations, since the previous results cannot be manufactured with available tool sets. Instead, starting parameters were chosen which used parameter sets of available tool sets taken from the IUL, TU Dortmund University. Nonetheless, the optimal solution of process parameters resulted in a set of parameters, which not directly coincided with available tool sets. Consequently, the results were approximated with available tools and the specimen manufactured and afterwards tested in SEM by project A02. The results from the experiments coincided with the simulated results, drastically reducing the damage within the analyzed area, see Fig. 4. This successful validation further proves the applicability of the developed optimization framework.
Concluding, the examples demonstrate the applicability of the developed industrial optimization strategy to the class of bulk forming. The results indicated that application of such optimization strategies may yield interesting and not necessarily intuitively derivable results.
 |
|
Fig. 4.: a) Initial and b) optimal setup for forward hollow extrusion. c) The validation using the approximated set of parameters and the data from the SEM analysis. |
Optimization with commercial software: stretch indenting
The second optimized forming process was achieved in cooperation with project A06. To reduce computation time, the process of stretch indenting was chosen to be optimized, as it allowed a reduction to 2d simulations. The material model used within the simulation was an adapted Lemaitre model derived and calibrated in the first funding period by project S01. The process itself consisted of a punch, a die with a draw bead, a blank holder with an indentation for the draw bead and the sheet. Since a damage model was used, the objective was chosen to use the damage variables computed within the simulations.
 |
|
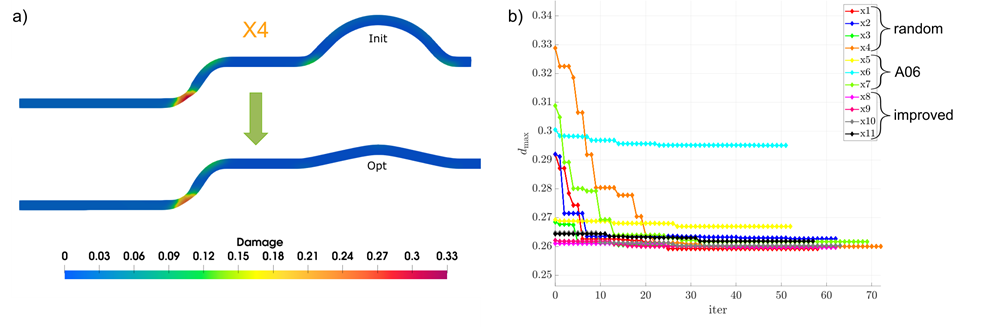
Fig. 5.: Optimization of stretch indenting. a) The initial and optimal sheet x4 and b) the objectives over iterations. |
Two different optimization problems were stated, where the first used an accumulated quantity like in the optimization of the variational derived gradients for the C02 model and the second used the maximum damage value dmax. Both optimizations however, yielded similar results. The optimization itself aimed to reduce the objective by altering the shape of the drawbead and with it the flow of the material. Three parameters were required to define the draw bead. Two radii which shaped the draw bead, as well as the parameter hs, which describes the vertical offset of the lower radius. Additionally, the shape of the drawbead was constrained by geometric and process bounds. Consequently, the draw bead had to be higher than the metal sheet and must not exceed a certain threshold, and finally it had to fit into the die with manufacturing tolerances to either side. These constraints were added to the optimization, which significantly reduced the design space.
The optimizations were run with three different sets of starting guesses. The first set with four optimizations used random start parameters, see Fig. 5, while the second set of optimizations used starting parameters provided by project A06, which categorized the draw bead into a “smallest”, an “average” and a “biggest” variant. All seven of these optimizations, with the exception of set 6, which ran into a local minimum, converged to similar values of dmax ≈ 0.26. While the combination of radii, as well as parameter hs, differed between all solutions, their common feature was the draw bead height ys. A minimization of this parameter coincided with a minimization of damage within the sheet material. Based on this research, a final set of four optimizations were conducted, which used start parameters close to the optimal value for ys = 2 mm, aiming to find better a combination of process parameters. However, while a better value for dmax could be found, the effect was negligible small, such that the previous conclusion describes the outcome of the optimization accurately.
Concluding, the examples demonstrate the applicability of the developed industrial optimization strategy to the class of sheet metal forming. Additionally, this example highlights the benefit of such an optimization in the sense that it may result in universal statements regarding parameter combinations.
Transfer of deterministic sensitivity analysis to future project C06
The expiring project C05 focused on algorithmic development for efficient determination of local sensitivity information and optimization of damage related system responses regarding process parameters in forming processes in an overall deterministic setting [*Guh23a,b,c]. The future project C06, directed by Prof. Faes, will focus on robust design optimization considering uncertainties and variabilities, i.e. probabilistic models and global sensitivity methods will be used, cf. [Fae18,Fae20,Val21,Val23]. However, to benefit from both scientific fields and to ensure a smooth transfer of knowledge, the two groups started cooperating especially on topics like gradient enhanced neural networks, as well as the utilization of local sensitivity information in the context of uncertainty quantification and reliability analysis. On the one hand, local sensitivity information can be used to increase the prediction accuracy and training efficiency of deep neural networks. On the other hand, this information can be beneficial for the selection of design parameters in view of global sensitivity methods. To this end, project C05 provided the work group of Prof. Faes with sensitivity data and software to enable and support their research.
| [Spr20] | Sprave, L., Menzel, A. A large strain gradient-enhanced ductile damage model: finite element formulation, experiment and parameter identification. Acta Mech 231 (2020) 5159–5192. |
| [Her20] | Hering, O., Tekkaya, A.E.: Damage-induced performance variations of cold forged parts. Journal of Materials Processing Technology 279 (2020) 116556 |
| [Fae18] |
Faes, M., Van Doninck, B., Imholz, M. and Moens, D.: Product reliability optimization under plate sheet forming process variability. 8th International Workshop on Reliable Computing, Liverpool, United Kingdom (2018) |
| [Fae20] | Faes, M., Valdebenito, M.: Fully Decoupled Reliability-Based Design Optimization of Structural Systems Subject to Uncertain Loads. Comp. Meth. in Appl. Mech. and Eng. 371 (2020) 113313 |
| [Val21] | Valdebenito, M., Misraji, M, and Jensen, H, and Mayorga, F.: Sensitivity estimation of first excursion probabilities of linear structures subject to stochastic Gaussian loading. Computers & Structures 248 (2021) 106482 |
| [Val23] | Valdebenito, M., Faes, M., Misraji, M. and Jerez, D.: First Excursion Probability Sensitivity Estimation by means of Multidomain Line Sampling. In Proc: ICASP14, Dublin, Ireland (2023) |
| [*Guh19a] | Guhr, F., Barthold F.-J., Meya, R., Tekkaya, A. E.: Load Optimisation for Air Bending in the Context of Damage Reduction. Proc. Appl. Math. Mech. 19: e201900179 (2019) |
| [*Guh19b] | Guhr, F., Barthold, F.-J.: Proc. 8th GACM (2019) 55–58, Kassel, Germany |
| [*Guh20] | Guhr, F., Sprave, L., Barthold, F.-J., Menzel, A.: Computational shape optimisation for a gradient-enhanced continuum damage model. Comput Mech 65 (2020) 1105–1124 |
| [*Guh21a] | Guhr, F. and Barthold, F.: Damage Optimisation for Air Bending. Proc. Appl. Math. Mech., 20: e202000074 (2021) |
| [*Guh21b] | Guhr, F. and Barthold, F.-J.: Shape optimised geometries for ductile damaging materials. Proc. Appl. Math. Mech., 21: e202100198 (2021) |
| [*Guh23a] | Guhr, F. and Barthold, F.-J.: Geometric and material sensitivities for elasto-plasticity including non-local damage regularisation. Proc. Appl. Math. Mech., 23: e202200233 (2023) |
| [*Guh23b] | Guhr, F. and Barthold, F.-J.: Variational sensitivity analysis and shape optimisation applied to a non-local, ductile damage model. Comput Mech (2023) (online) |
| [*Guh23c] | Guhr, F., Gitschel, R., Barthold, F.-J. and Tekkaya, A.E.: Numerical Optimisation of Damage in Extrusion Processes. Proc. Appl. Math. Mech., 24: 202300199 (2024) |
| [*Lie20] |
Liedmann, J., Gerke, S., Barthold, F.-J., and Brüning, M..: Shape optimization of the X0-specimen: theory, numerical simulation and experimental verification. Comput Mech 66 (2020) 1275-1291 |