Summary
The formability of polycrystals at the macroscale is defined by deformation and damage mechanisms at the microscale. To describe such mechanisms, a crystal plasticity theory has been coupled with interface models and integrated into representative volume elements (RVEs) during the 1st funding period (FP) and the 2nd FP. The interface models capture decohesion at the grain boundaries as well as the initiation and propagation of micro-cracks (damage) within the quasi-brittle martensite phase of the dual phase steel DP800.
The contribution of project C04 to the overall TRR 188 is manifold. Starting from materials characterization at the microscale (project area B) and in line with a bottom-up-approach, fundamental physical parameters such as critical resolved shear stresses or fracture energies of the involved interfaces can be directly integrated into the model. Still following a bottom-up-approach – the resulting RVE-model allows to compute effective macroscopic properties such as stress-strain relationships. These are used to develop and calibrate macroscopic models (project area C) as well as to analyze the effect of different load paths on the effective mechanical properties. By doing so, improved load paths can be identified that, in turn, support the identification of novel process parameters (project area A). In line with the 1st FP and the 2nd FP, project C04 remains to be characterized by its unique bridging function across scales and between characterization and forming processes.
The objectives of the 3rd FP are driven by the TRR 188 overall goals advanced phenomena, increasing complexity of forming processes and tailoring damage-tolerant materials. Concerning the first two of these goals, temperature- and pressure-induced healing will be included in the model. By doing so, thermomechanically coupled RVE computations will allow to estimate whether healing or further damage evolution occurs under certain load paths and subsequently, to identify improved loading and process parameters. Furthermore, project C04 will also assist to analyze the performance of pre-damaged parts under operational loading conditions by implementing fatigue indicators. Finally, the framework to be elaborated will be adapted for other materials such as aluminum alloys. Since RVE-computations are numerically very expensive, simplified models shall be developed. Particularly, the crystal plasticity model shall be approximated. Since the numerical complexity of the resulting RVE model will still not allow for congruent multi-scale simulation of forming processes, effective, macroscopic forming-induced damage tensors are to be derived by means of computational homogenization. These tensors will further improve the macroscopic models as well as provide realistic initial conditions for fatigue analyses. Furthermore, sensitivity analyses of the damage evolution shall be carried out. Important influencing variables such as the stress triaxiality or the Lode parameter will be explicitly controlled. This allows deriving technologically relevant simplified damage indicators to estimate which mechanism is most dominant – a core task of the TRR 188.
Report and current state of research
The aim of the 1st FP was to develop finite element models for Representative Volume Elements (RVE) of the materials considered in the TRR 188. In addition to inelastic deformations caused by plastic gliding at the slip planes within the individual grains of the polycrystal, damage at the grain boundaries was also taken into account. The resulting micromechanical model allowed to analyze the interaction between the aforementioned mechanisms (plastic slip vs. decohesion at the grain boundaries) for complex load paths characterizing forming processes such as deep drawing.
In the 2nd FP, (1) a direct connection to project area B was realized by using observable / measurable variables within the crystal plasticity model, (2) micro-cracks in the quasi-brittle martensite grains – an additional and important damage mechanism – were embedded into the RVE model, (3) the scope of the RVE model was extended by considering additional effects such as rate-dependency and (4) the numerical efficiency and robustness of the finite element formulation was significantly improved. While the connection of the first three of these points to the TRR 188 is obvious, point (4) is mandatory for tackling the time-and hardware-consuming RVE-simulations.
In what follows the results obtained during the 2nd FP and the newly developed methods are summarized. This section is organized according to the underlying mechanical models. This leads to the following structure:
- Crystal plasticity model
- Rate-independent and rate-dependent hardening models based on dislocation densities
- Efficient algorithmic formulations for rate-independent models
- Interface / cohesive zone models
- Additional damage mechanism: micro-cracking in quasi-brittle martensite grains
- Extended model for decohesion at grain boundaries: rate-effects
- Sensitivity analyses regarding the interaction and activation of the different (damage) mechanisms
Crystal plasticity model: Fundamentals
Since the effective response of the RVE results from an interplay between inelastic deformations within the individual grains, decohesion at the grain boundaries and micro-cracking in the quasi-brittle martensite grains, each of these mechanisms must be captured in a physically sound and numerically efficient manner. First, the results with respect to crystal plasticity theory are presented.
The foundations of the crystal plasticity framework have been laid already within the 1st FP and are briefly summarized in this paragraph. The two key features of this framework are: the incorporation of gradient hardening by means of the so-called micromorphic approach (see [For09]) and a variationally consistent thermomechanical coupling in line with [Yan06] and further elaborated in [*Bar15]. Following [*Foh18a], the resulting model is driven by energy minimization (or stationarity; see also [Ort99] and [Car02] for further details on incremental variational principles) and allows to predict the temperature increase caused by plastic deformations realistically and thermodynamically consistently, cf. [*Bar15]. According to [*Foh18a], the associative gradient-enhanced crystal plasticity framework is defined by yield functions (or equivalently by dissipation functionals) and a Helmholtz energy. The structure of the latter reads in the isothermal setting
| (1) |
where Fe and Fp are the elastic and the plastic part of the deformation gradient, α is a vector containing the accumulated plastic slip at each plane and s is its micromorphic counterpart. Identity s = α is approximated by penalty energy ψpenalty. Accordingly, local hardening is captured by ψp,loc, while nonlocal gradient-hardening is governed by ψp,nonl. Finally, the elastic response is defined by ψe.
Crystal plasticity model: Dislocation density-based hardening
Although the model indeed accounts for gradient hardening, the respective energy can only be identified indirectly, e.g., by comparing model predictions to experiments for specimens having different sizes. Alternatively, if hardening model/energy ψp,nonl was based on dislocation densities, measurements such as those conducted in projects B03 and B04 could be directly used. Exactly this idea was pursued in the 2nd FP. For that purpose, the gradient of variable , is decomposed into one part related to (geometrically necessary) edge dislocations and another part corresponding to (geometrically necessary) screw dislocations, cf. [Gur05]. Following [Gur05], an approximate relation for small slip rates is employed, since this approximation allows to eliminate the dependence of on the plastic part of the deformation gradient. By doing so, the dislocation density-based model is indeed characterized by an energy of type (1). A finite element computation of this model for a single crystal is shown in Fig. 1, cf. [*Foh24].
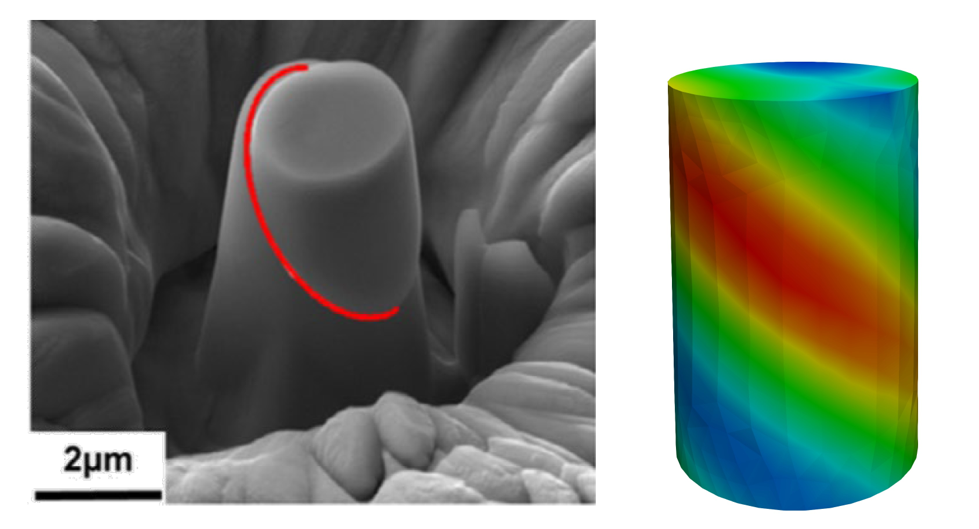 |
| Fig. 1: Micropillar compression: (left) experiment (project B03) vs. (right) dislocation density-based hardening finite element model (distribution of accumulated plastic strain) |
Crystal plasticity model: Rate-effects – Viscoplasticity
The dislocation density-based crystal plasticity theory outlined in the previous paragraph facilitated the development of improved hardening models on the one hand. On the other hand, it also improved the link to project area B. The same link also motivated the incorporation of rate-effects into the model. For this reason, viscoplastic extensions of the model were elaborated in the 2nd FP. By doing so, the range of applications of the final model was further broadened – in line with the advanced process technologies developed in project area A.
Several different viscoplasticity models were implemented and analyzed. While most of them are able to capture the rate-dependent response of crystals, they differ considerably with respect to their rate-independent limiting case as well as their numerical efficiency and robustness. Among the different models, the one proposed in [Cui93] was chosen. According to [*Nie23], it can be written in the time-discretized, residual form
| (2) |
where τ(i) is the Schmid stress and Q0 - Q is the current yield stress at slip plane (i), Δλ = [Δλ(1),...,Δλ(n)] is the collection of all integrated plastic multipliers, Δt is the time increment and n and η are a rate-exponent and a viscosity parameter. This model consistently converges to the rate-independent limit (e.g., if η → 0) and it is numerically robust and efficient; see also the discussion in [Prü20]. Furthermore, it can be recast into a variational structure by defining a dissipation functional, cf. [Ort99]. In collaboration with project B03, the model parameters were identified based on micropillar test. The results are summarized in Fig. 2.
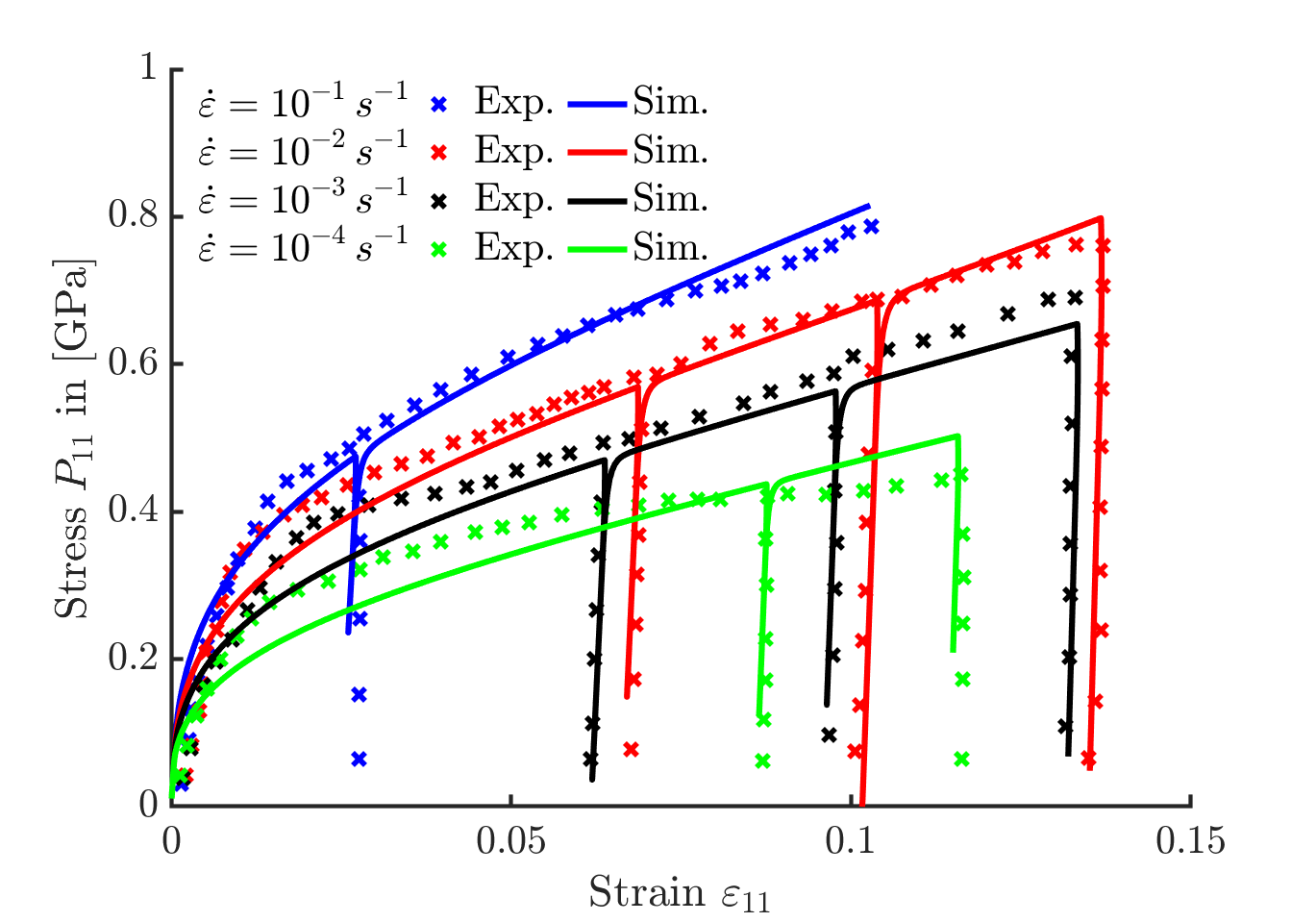 |
| Fig. 2: Rate-dependence of the ferrite phase within the dual-phase steel DP800. The strains are computed from the top-displacement of the micropillar including the substrate: Experiment vs. Simulation |
Rate-dependent extensions such as those described in the previous paragraph often serve two purposes. The first of those is obvious: capturing the viscoplastic response of a single crystal or a polycrystal. However, viscoplastic models are also often employed for approximating the rate-independent limiting case, cf. [Prü20] and [*Nie23]. For that purpose and following a penalty formulation, the rate-sensitivity is iteratively reduced. Although this straightforward idea is indeed tempting, it is debatable for – at least – two reasons.
First, the beneficial effect of a (numerical) viscosity is not present for very slow processes and furthermore, combining or mixing a physics-motivated viscosity with a numerically-motivated one is problematic, since both effects cannot be separated in general and hence, they interfere, cf. [*Lan22]. Second, classic penalty methods are known to show significant drawbacks compared to more advanced optimization methods, see [Gei99]. For these reasons, numerically robust and efficient algorithms for rate-induced crystal plasticity theory are still required. Although this has been known for a long time, there is still a need for research in this respect. In this context, it should be emphasized that the numerical simulations based on RVEs, which are centrally embedded in the TRR 188, are only made possible by such state-of-the-art formulations.
Crystal plasticity model: Efficient algorithmic formulations for rate-independent models
Due to the importance of this working package – RVE simulations are only possible if the underlying crystal plasticity model is numerically robust and efficient – it started already during the 1st FP. The overriding idea has been to exploit the underlying variational structure of crystal plasticity theory. This structure allows to employ powerful techniques from non-linear constrained optimization methods (see, e.g. [Gei99]) for solving the mathematical problem of crystal plasticity theory. In what follows, three such techniques are presented.
The first powerful technique from non-linear constrained optimization is the family of nonlinear complementarity problems (NCP) functions. By using these functions, the inequalities characterizing rate-independent elasto-plasticity can be replaced by equalities. Two different NCP functions were analyzed in detail and further elaborated. The first of those is the (regularized) Fischer-Burmeister function. This function was applied to crystal plasticity theory in [Bal03] for the first time and analyzed in [*Foh18b]. However and in contrast to [Bal03] and also [*Foh18b], a rescaled extension of this function was proposed by the applicants, cf. [*Foh24]. This function reads for slip system (i)
| (3) |
where Φ(i) is the yield function, is the integrated plastic multiplier, Δλ(1) is a small numerical parameter regularizing the non-smoothness of the function and δ is a novel weighting parameter. By setting δ = 0, Eq. (3) is equivalent to the classic loading/unloading conditions Φ(i) ≤ 0, Δλ(1) ≥ 0 and Φ(i)Δλ(1) = 0. According to [*Foh24], the resulting system of equations defining crystal plasticity theory shows a regular tangent matrix, if parameters δ and ω are chosen properly – in sharp contrast to a conventional implementation, see Fig. 3. Recommendations for the choice of and are also given in [*Foh24]. In addition to the Fischer-Burmeister function, the frequently employed min-function was also considered. However, this function is not able to regularize the ill-posed equations of rate-independent crystal plasticity theory. As a matter of fact, it was shown in [*Foh24], that an implementation based on the min-function is equivalent to a classic active set algorithm. In summary, the novel algorithm based on the rescaled extension of the Fischer-Burmeister function approximates the equations of crystal plasticity theory and leads to a regular tangent. To be more specific, the algorithm solves the problem of identifying the active set, its tangent is regular and it is numerically extremely efficient. Unfortunately, it is sometimes not robust enough. More precisely, numerical experiments revealed that the algorithm sometimes does not converge for large load increments – even if it is combined with line search strategies and other techniques known from globally convergent schemes, cf. [Gei99].
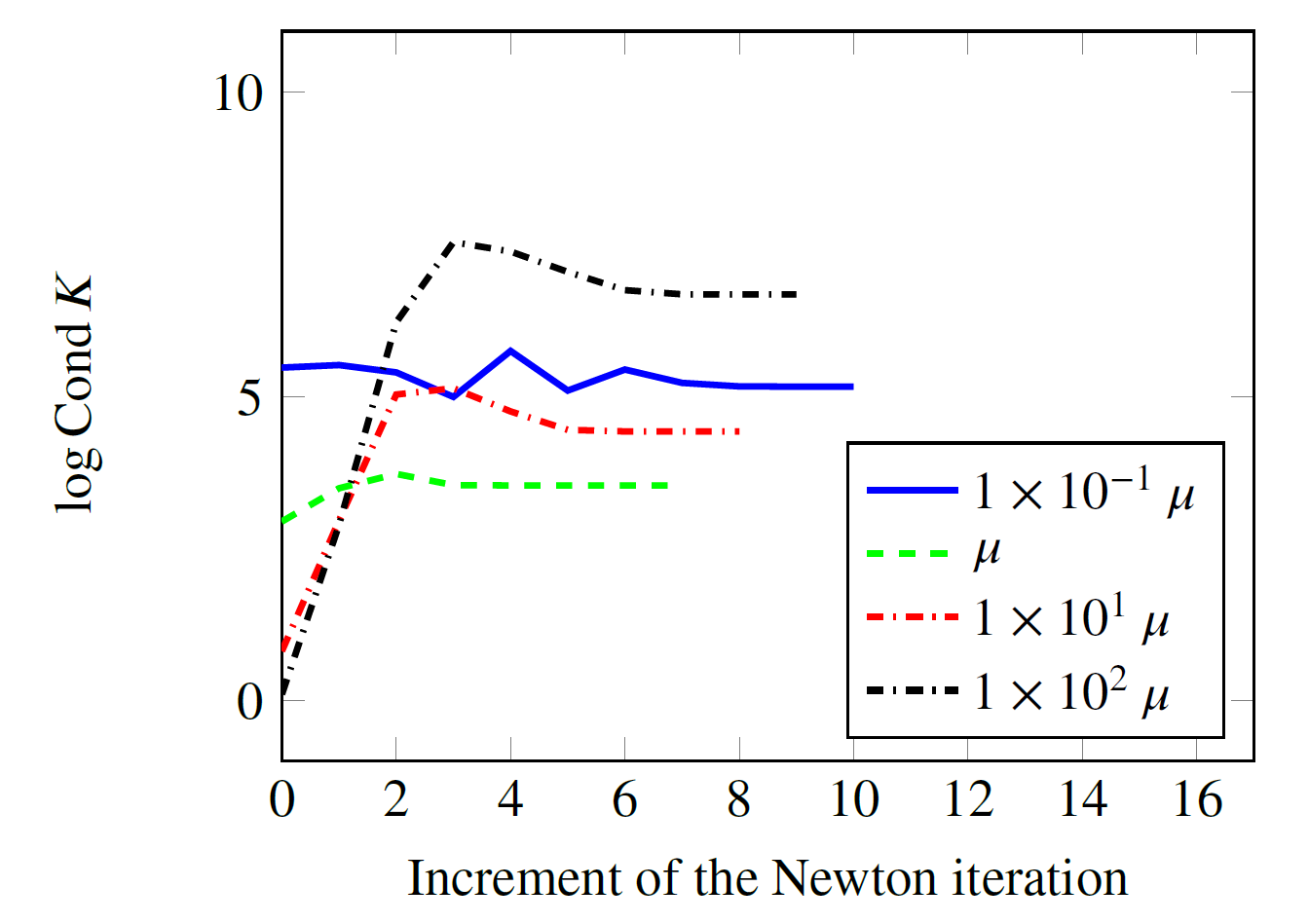 |
| Fig. 3: Effect of weighting parameter (see Eq. (2) and [*Foh24]) within the modified Fischer-Burmeister-function on the condition number Cond K of the algorithm |
Due to the aforementioned restrictions of the Fischer-Burmeister function with respect to the load increment size, another effective method from non-linear constrained optimization was also studied and implemented: an algorithm based on the augmented Lagrangian approach. As far as crystal plasticity is concerned, this idea was again proposed for crystal plasticity in [Bal03] for the first time. The combination of the penalty scheme and the Lagrange method leads to a viscoplastic regularization of the underlying rate-independent problem. However, if the regularization/penalty parameter is sufficiently large (but still finite), the solution is independent with respect to this parameter – in contrast to the penalty method, cf. [Gei99]. The algorithm presented in [Bal03] was further extended by the applicants. Particularly, more efficient techniques for computing the tangent matrix were developed and more efficient termination criteria for the inner loop of the augmented Lagrangian scheme (Newton iteration) were analyzed. The resulting algorithm is extremely robust – even for large loading increments. However, although that is frequently claimed, the algorithm does not eliminate the singularity of the equations defining rate-independent crystal plasticity theory. The singularity is only eliminated by a classic penalty approach. For the sake of comparison, this classic penalty approach was also implemented. It is based on the rate-dependent crystal plasticity model described before; see Eq. (2). However, the viscosity parameter is iteratively decreased.
Finally, inspired by [Sch20] and [Sch21], the interior-point method was also employed for solving the non-linear constrained optimization problem characterizing (rate-independent) crystal plasticity theory. The final algorithm developed by the applicants and published in [*Nie23] is a significant improvement compared to the previous works in [Sch20] and [Sch21]. The most important features of the novel algorithm are: (1) the introduction of slack variables in order to check and enforce feasibility, (2) an efficient and robust line search procedure to ensure strict feasibility throughout the iterations, (3) avoiding the inherent ill-conditioning of the barrier approach by rewriting the residual equation, (4) analysis of different preconditioning and factorization techniques in order to improve the efficiency and the robustness of the algorithm and (5) an adaptive strategy for decreasing the barrier parameter to obtain fast convergence, together with the elaboration of termination criteria of the inner Newton iterations in order to further improve the efficiency of the algorithm. The effect of the novel developments is shown in Fig. 4. According to this figure, the aforementioned rescaling indeed has a significant impact on the performance, since it affects the condition number (note that the y-axis of the diagram scales logarithmically).
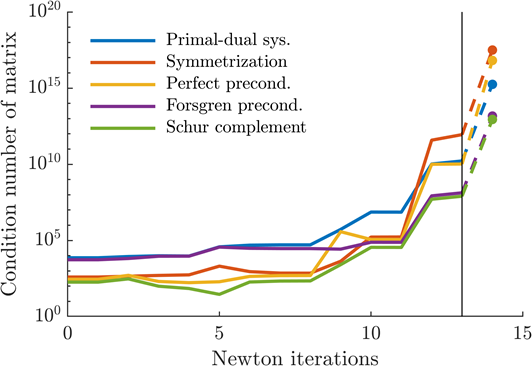 |
| Fig. 4: Interior-point method for solving crystal plasticity theory, cf. [*Nie23] – simple shear test: Evolution of the condition number for different rescaling strategies |
The working package dealing with efficient algorithmic formulations for rate-independent models is now completed. The most important observations are: (1) the implementation based on the (regularized) Fischer-Burmeister function is the fastest one (walltime). However, it is not the numerically most robust scheme. For this reason, it is currently combined with the interior-point method or the augmented Lagrangian approach. The latter is only used, if the Fischer-Burmeister function does not converge. Finally, it is mentioned that the different algorithms might converge to different solutions (the optimization problem of crystal plasticity theory is highly non-convex), cf. [*Nie23]. The applicants are going to analyze these differences with respect to physics in the future – however, not within the scope of the TRR 188, but in a separate project.
Interface / cohesive zone models
While plastic deformations within the individual grains of the polycrystal are modeled by means of crystal plasticity theory, damage at the microscale has been considered at the grain boundaries during the 1st FP. For that purpose, the general cohesive zone framework originally developed in [*Ott16] and embedded into computational homogenization theory in [*Hei21] was employed. This framework allows to represent arbitrary material anisotropies. Moreover, it fulfills the fundamental physical conservation laws such as balance of angular momentum – in contrast to previously published interface models. Furthermore, decohesion mechanisms as well as effects due to surface tension are consistently included in the model. Although the range of applications of this model is already very broad, it was further extended to take also rate-effects into account – in line with the projects of the A area dealing with process technologies. This extension was implemented within the variational interface model by adding a dissipation potential which is not anymore positively homogeneous of degree one, cf. [Ort99] and [*Lan22]. The identification of the associated model parameters is still pending and will be realized by a collaboration with project B03. It should be noted that strong synergies exist with project B01 where cohesive zone models are also developed.
According to the experiments conducted in project B02, damage in the TRR 188 model industrial DP steel is not limited to the grain boundaries, but rather occurs predominantly within the quasi-brittle martensite phase. As a consequence, this additional mechanism has also been integrated into the micromechanical model. Since the spatial distribution of damage in the quasi-brittle martensite phase is not known beforehand (in contrast to decohesion which is always located at the grain boundaries), a phase-field model was employed, see [Bou00]. It is based on the works [*Bod23] and [*Lam23] of the applicant. In contrast to the pioneering work [Bou00], the phase-field extension in [*Lam23] allows to include any traction-separation law (sharp interface model) into the phase-field approximation (diffuse interface), see also [Con16]. Particularly, the fracture energy as well as the strength of the material interface can be prescribed. A structural analysis based on this novel framework is shown in Fig.5. Alternative engineering approximations of cohesive zone models can be found in [Wu17] and [Lor12] – however, based on a one-dimensional comparison and without any rigorous mathematical proof.
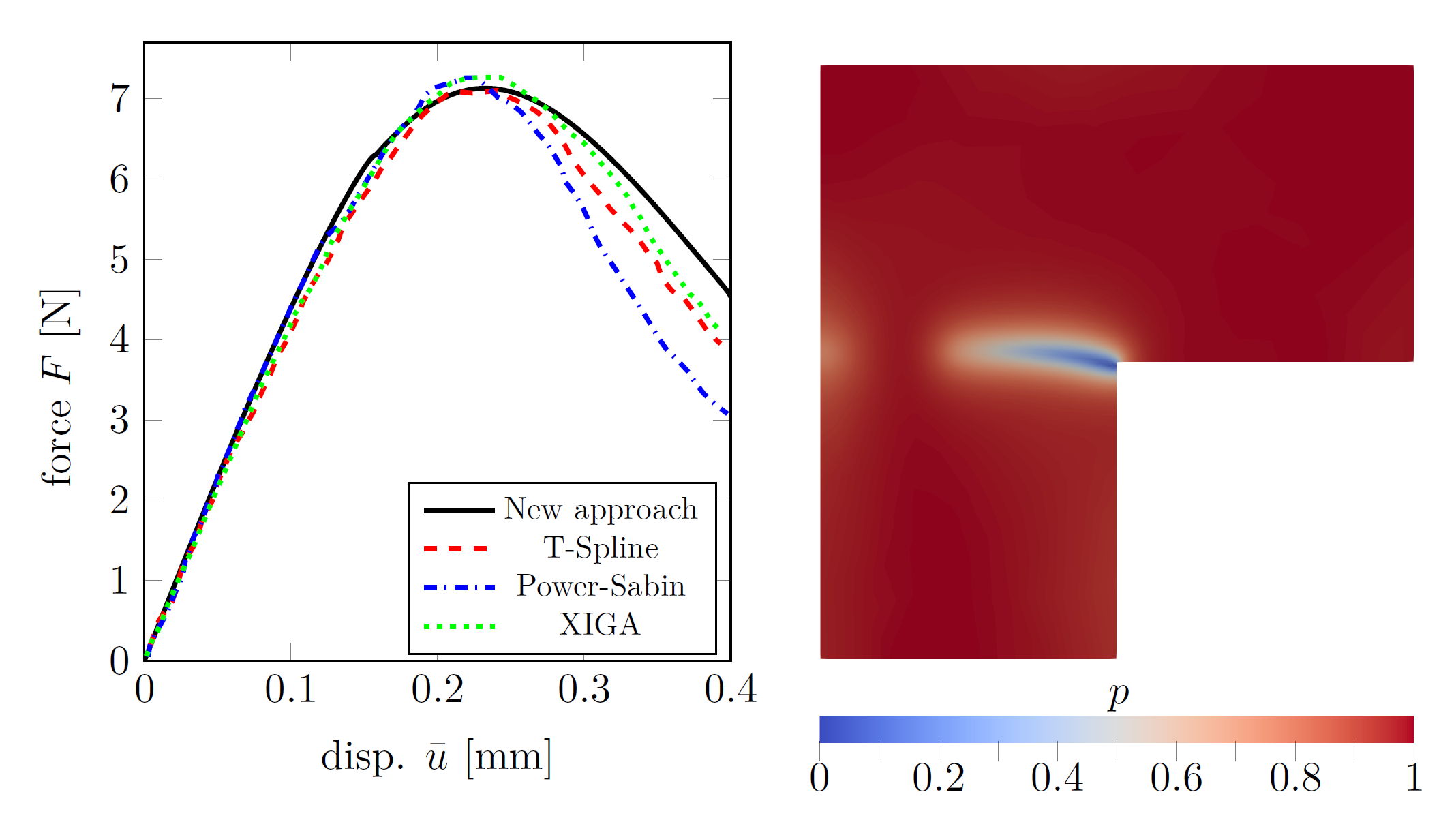 |
| Fig. 5: Finite element phase-field approximation of cohesive zone models, cf. [*Lam23]. Numerical analysis of an L-shaped plate: (left) Force displacement diagram predicted by the novel model and predictions taken from [Fat20] and (right) phase-field distribution at the final stage (p=1-damage). |
It bears emphasis that phase-field computations are extremely challenging, since the non-convexity of the underlying potential/energy leads to severe problems. These problems are also expressed in multiple solutions resulting in the so-called brutal crack growth, i.e., the speed of the crack growth might be infinity in the case of rate-independent functionals. For this reason, advanced numerical schemes are necessary, cf. [Bou07] and [Ger16]. Recently, a mathematically sound and efficient algorithm was proposed by the applicant, [*Bod23]. It is based on an alternate minimization, in combination with a (pseudo)viscosity. As shown in [*Bod23], the algorithm consistently approximates so-called Balanced Viscosity (BV) solutions which are known to exhibit physically sound properties. Particularly, BV-solutions are defined by energetically optimal trajectories which do not jump across energy barriers. From a more practical point of view, the algorithm presented in [*Bod23] is very robust.
Sensitivity analyses regarding the interaction and activation of the different (damage) mechanisms
The crystal plasticity model and the two interface models (decohesion at the grain boundaries and damage in the quasi-brittle martensite phase) developed during the first two funding periods have been incorporated into RVEs characterizing the dual phase steel DP800. Finite element analyzes of such RVEs serve, at least, two purposes: (1) identification of improved load paths as well as microstructures that favor a certain damage mechanism (decohesion vs. damage in quasi-brittle martensite phase) and (2) computation of effective macroscopic properties such as stress-strain relations or also effective damage tensors. The link of project C04 to project area A is thus obvious: The aforementioned RVE-computations provide guidelines for choosing appropriate process parameters, i.e., the effect of different load paths on the resulting effective macroscopic mechanical behavior can be analyzed. However, the computation of effective macroscopic parameters and the forming-induced ductile damage is also important for the development of novel macroscopic models (such as those of C01 and C02). The central role of project C04 within the TRR 188 is thus clearly visible. An example highlighting the effect of the two most important damage mechanisms is given in Fig. 6. Such RVE-computations will continue to be one of the core tasks of Project C04 in the 3rd FP.
 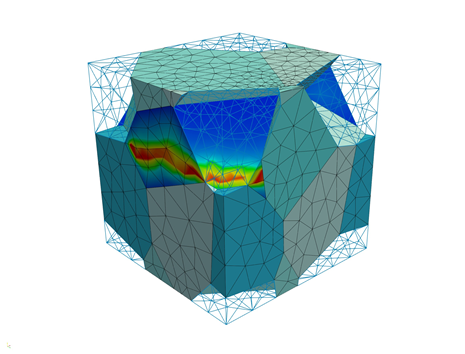 |
| Fig. 6: FE-simulation of an RVE (dual steel DP800): (left) failure resulting from decohesion at the grain boundaries (interface elements) and (right) failure driven by micro-cracking in the quasi-brittle martensite (phase-field model) |
Project- and subject-related list of publications
| [*Bar15] | Bartels, A.; Bartel, T.; Canadija, M.; Mosler, J.: On the thermomechanical coupling in dissipative materials: A variational approach for generalized standard materials. Journal of the Mechanics and Physics of Solids 2015; 82:218-234. https://doi.org/10.1016/j.jmps.2015.04.011 |
| [*Bod23] | Boddin, S.; Rörentrop, F.; Knees, D.; Mosler, J.: Approximation of balanced viscosity solutions of a rate-independent damage model by combining alternate minimization with a local minimization algorithm, 2023. https://doi.org/10.48550/arXiv.2211.12940 |
| [*Foh18a] | Fohrmeister, V.; Bartels, A.; Mosler, J.: Variational updates for thermomechanically coupled gradient-enhanced elastoplasticity – Implementation based on hyper-dual numbers. Computer Methods in Applied Mechanics and Engineering 2018; 339:239–261. https://doi.org/10.1016/j.cma.2018.04.047 |
| [*Foh18b] | Fohrmeister, V.; Diaz, G.; Mosler, J.: Classic crystal plasticity theory vs crystal plasticity theory based on strong discontinuities – Theoretical and algorithmic aspects. International Journal for Numerical Methods in Engineering 2018; 30:1283-1303. https://doi.org/10.1002/nme.6000 |
| [*Foh24] | Fohrmeister, V.; Mosler, J.: Rate-Independent Gradient Crystal Plasticity Theory – Robust Algorithmic Formulations based on Incremental Energy Minimization. International Journal of Solids and Structures 2024; 288:112622. https://doi.org/10.1016/j.ijsolstr.2023.112622 |
| [*Hei21] | Heitbreder, T.; Kurzeja, P.; Mosler, J.: On general imperfect interfaces with spatially non-constant displacement jumps. International Journal of Solids and Structures 2021; 232:111068. https://doi.org/10.1016/j.ijsolstr.2021.111068 |
| [*Lam23] |
Lammen, H.; Conti, S.; Mosler, J.: A finite deformation phase field model suitable for cohesive fracture. Journal of the Mechanics and Physics of Solids 2023: 178:105349. https://doi.org/10.1016/j.jmps.2023.105349 |
| [*Lan22] | Langenfeld, K.; Kurzeja, P.; Mosler, J.: How regularization concepts interfere with (quasi-)brittle damage: a comparison based on a unified variational framework. Continuum Mechanics and Thermodynamics 2022; 34:1517-1544. https://doi:10.1007/s00161-022-01143-2 |
| [*Nie23] | Niehüser, A.; Mosler, J.: Numerically efficient and robust interior-point algorithm for finite strain rate-independent crystal plasticity. Computer Methods in Applied Mechanics and Engineering 2023; 416:116392. https://doi.org/10.1016/j.cma.2023.116392 |
| [*Ott16] | Ottosen, N. S.; Ristinmaa, M.; Mosler, J.: Framework for non-coherent interface models at finite displacement jumps and finite strains. Journal of the Mechanics and Physics of Solids 2016; 90: 124-141. https://doi.org/10.1016/j.jmps.2016.02.034 |
| [Als15] | Alsheghri, A. A.; Al-Rub, R. K. A.: Thermodynamic-based cohesive zone healing model for self-healing materials. Mechanics Research Communications 2015; 70:102-113. https://doi.org/10.1016/j.mechrescom.2015.10.003 |
| [Bal03] | Schmidt-Baldassari, M.: Numerical concepts for rate-independent single crystal plasticity. Computer Methods in Applied Mechanics and Engineering 2003; 192:1261-1280. https://doi.org/10.1016/S0045-7825(02)00563-7 |
| [Ble13] | Bleier, N.; Mosler, J.: A hybrid variationally consistent homogenization approach based on Ritzs method. International Journal for Numerical Methods in Engineering 2013; 94:625-647. https://doi.org/10.1002/nme.4465 |
| [Bou00] | Bourdin, B.; Francfort, G.; Marigo, J.-J.: Numerical experiments in revisited brittle fracture. Journal of the Mechanics and Physics of Solids 2000; 48: 797–826. https://doi.org/10.1016/S0022-5096(99)00028-9 |
| [Bou07] | Bourdin, B.: Numerical implementation of a variational formulation of quasi-static brittle fracture. Interfaces Free Bound. 2007; 9:411–430. https://doi:10.4171/IFB/171 |
| [Car02] | Carstensen, C.; Hackl, K.; Mielke, A.: Non-convex potentials and microstructures in finite-strain plasticity. Proc. R. Soc. Lond. A 2002; 458: 299-317. https://doi.org/10.1098/rspa.2001.0864 |
| [Con16] | Conti, S.; Focardi, M.; Iurlano, F: Phase field approximation of cohesive fracture models. Annales de l'Institut Henri Poincaré C, Analyse non linéaire. 2016; 33:1033-1067. https://doi.org/10.1016/j.anihpc.2015.02.001 |
| [Cui93] |
Cuitino, A. M.; Ortiz, M.; Computational modelling of single crystals. Modelling and Simulation in Materials Science and Engineering 1993; 1:225. https://doi.10.1088/0965-0393/1/3/001 |
| [Fat20] | Fathi, F.; Chen, L.; de Borst, R.: Extended isogeometric analysis for cohesive fracture, International Journal for Numerical Methods in Engineering 2020; 121:4584–4613. https://doi.org/10.1002/nme.6453 |
| [For09] | Forest, S.: Micromorphic Approach for Gradient Elasticity, Viscoplasticity, and Damage. Journal of Engineering Mechanics 2009; 135(3):117–131. https://doi.10.1061/(ASCE)0733-9399(2009) |
| [Gei99] | Geiger, C.; Kanzow, C.: Theorie und Numerik restringierter Optimierungsaufgaben. Springer 1999. |
| [Ger16] | Gerasimov, T.; De Lorenzis, L.: A line search assisted monolithic approach for phase-field computing of brittle fracture. Computer Methods in Applied Mechanics and Engineering 2016; 312:276-303. https://doi.org/10.1016/j.cma.2015.12.017 |
| [Gu19] | Gu, C.; Lian, J.; Bao, Y.; Münstermann, S.: Microstructure-based fatigue modelling with residual stresses: Prediction of the microcrack initiation around inclusions. Mat. Science & Engineering A 2019; 751:133-141. https://doi.org/10.1016/j.msea.2019.02.058 |
| [Gur05] | Gurtin, M.: The Burgers vector and the flow of screw and edge dislocations in finite-deformation single-crystal plasticity. Journal of the Mechanics and Physics of Solids 2006; 54:1882-1898. https://doi.org/10.1016/j.jmps.2006.03.003 |
| [Lor12] | Lorentz, E.; Cuvilliez, S.; Kazymyrenko, K.: Modelling large crack propagation: from gradient damage to cohesive zone models. International Journal of Fracture 2012; 178:85–95. https://doi.org/10.1007/s10704-012-9746-7 |
| [Ort99] | Ortiz, M.; Stainier, L.: The variational formulation of viscoplastic constitutive updates. Computer Methods in Applied Mechanics and Engineering 1999; 171:419-444. https://doi.org/10.1016/S0045-7825(98)00219-9 |
| [Pin14] | Pino-Muñoz, D.; Bruchon, J.; Drapier, S.; Valdivieso, F.: Sintering at Particle Scale: An Eulerian Computing Framework to Deal with Strong Topological and Material Discontinuities. Archives of Computational Methods in Engineering 2014; 21:141-187. https://doi.org/10.1007/s11831-014-9101-4 |
| [Prü20] | Prüger, S.; Kiefer, B.: A comparative study of integration algorithms for finite single crystal (visco)plasticity. International Journal of Mechanical Sciences 2020; 180:105740. https://doi.org/10.1016/j.ijmecsci.2020.105740 |
| [Sch20] | Scheunemann, L.; Nigro, P.; Schröder, J.; Pimenta, P. A.: A novel algorithm for rate independent small strain crystal plasticity based on the infeasible primal-dual interior point method. International Journal of Plasticity 2020; 124:1-19. doi: https://doi.org/10.1016/j.ijplas.2019.07.020 |
| [Sch21] | Scheunemann, L.; Nigro, P.; Schröder, J.: Numerical treatment of small strain single crystal plasticity based on the infeasible primal-dual interior point method. International Journal of Solids and Structures 2021; 232:111149. doi: https://doi.org/10.1016/j.ijsolstr.2021.111149 |
| [Sie20] |
Sievers, C.; Mosler, J.; Brendel, L.; Kurzeja, P.: Computational homogenization of material surfaces: From atomistic simulations to continuum models. Computational Materials Science 2020; 175:109431. https://doi.org/10.1016/j.commatsci.2019.109431 |
| [Voy12] |
Voyiadjis, G. Z.; Shojaei, A.; Li, G.; Kattan, P. I.: A theory of anisotropic healing and damage mechanics of materials. Proceedings: Mathematical, Physical and Engineering Sciences 2012; 468:163-183. https://doi.org/10.1098/rspa.2011.0326 |
| [Wu17] |
Wu, J.-Y.: A unified phase-field theory for the mechanics of damage and quasi-brittle failure, Journal of the Mechanics and Physics of Solids 2017; 103:72–99. https://doi.org/10.1016/j.jmps.2017.03.015 |
| [Yan06] | Yang, Q.; Stainier, L.; Ortiz, M.: A variational formulation of the coupled thermo-mechanical boundary-value problem for general dissipative solids. Journal of the Mechanics and Physics of Solids 2006; 54:401-424. https://doi.org/10.1016/j.jmps.2005.08.010 |
| [Zam10] | Zamiri, A.; Pourboghrat, F.; A novel yield function for single crystals based on combined constraints optimization. International Journal of Plasticity 2010; 26:731-746. https://doi.org/10.1016/j.ijplas.2009.10.004 |