Summary
Project C06 is aimed at optimizing the mechanical performance of metal formed parts through the robust design optimization of the manufacturing process in view of controlling and minimizing the damage and its variability. Hereto, state-of-the-art methods to quantify, propagate and optimize with uncertainties will be developed, implemented, and validated. Specific focus is placed on uncertainties in constitutive mechanical model parameters, geometry parameters, and manufacturing condition parameters for cold-forged 16MnCr5S steel parts and gas-based hot sheet metal formed aluminum. In parallel, developed methods will be also provided to the other sub-projects that deal with uncertainties (e.g., A02, A09, A10, B02, B03, and C02).
Based on this overarching goal, preliminary works were performed during the second funding period using) lump-sum funds. First, we assessed the feasibility of reducing the numerical costs of the non-linear finite element models used to simulate metal forming processes by means of a surrogate model. Specifically, both Gaussian Process regression and gradient-enhanced Deep Learning were assessed in collaboration with C05E, the predecessor project of the current C06N. It has been found that especially Gaussian Process regression offers a strong reduction in computational cost since it allows for active learning, reducing the training cost drastically since training points are selected in an optimal fashion. On top, it allows controlling the level of precision of the probabilistic descriptors being estimated. Also, in collaboration with C02 a preliminary study on the impact of parameter uncertainties on quantities driving damage was carried out using these surrogate modellign strategies, lying important preparatory work for the research project proposed herein. In the third funding period, the C06N project shifts the paradigm from performing optimization under the assumption that all required quantities can be perfectly quantified, to performing optimization under the full acknowledgment that uncertainties and variabilities are omnipresent in metal forming in view of reducing their effect on the final product. Hereto, we will further build on, and integrate the work of C05E project endeavors in terms of performing variational sensitivity analysis.
In the initial phase, knowledge and data on manufacturing uncertainty and material variability from subprojects A02, A09, B02, and B03 will be integrated into probabilistic mathematical models. These models will describe the variability in measured stress-strain relations of the 16MnCr5S material, incorporating typical uncertainties in environmental and manufacturing conditions using advanced probabilistic concepts. These uncertainty models will be integrated in collaboration with A02 into a numerical simulation model of the forward-rod extrusion process. Damage phenomena will be explicitly modeled by extending the C02 model to accommodate uncertainties, utilizing microstructural data from B03/B04 to construct random field representations of key mechanical quantities. The main challenges that will be tackled are the modelling of the uncertainties using data-driven random field approaches, as well as with the scarce nature of the data.
In a second phase of the project, advanced numerical schemes for the propagation of random fields through computationally expensive numerical models will be developed. This work package focuses on expanding surrogate modeling schemes based on Bayesian active learning applied in preliminary work to the C02 model in two ways. First, these models will be tuned to accurately identify the most influential uncertain quantities through variance-based sensitivity analysis. Second, to deal with random field-valued input quantities, as derived in the previous step, these methods need to be expanded from a theoretical viewpoint. With respect to the C05E project, these developments will assist the decision-making processes concerning optimal process parameters with integration of governing variabilities. Further, to determine the mechanical performance in terms of Charpy energy, the modified Bai-Wierzbicki (MBW) model of A09 will be integrated into the simulation.
The third phase of the sub-project will bring together these developments into a comprehensive framework that allows for optimizing the manufacturing process to jointly minimize the damage in the formed parts, as well as their scatter. Hereto, we will combine the developed active-learning schemes with decoupling approaches developed in prior work of the applicant. Not only will this increase the mechanical performance of the parts, it also will allow for manufacturing these high-quality parts more robustly. The developed framework will be applied to the airbag sleeve burst analysis optimization and the obtained reliability and robustness levels will be compared to the design of A09, as well as on the gas based hot sheet metal forming of aluminum (A10)
Current state of research and preliminary work
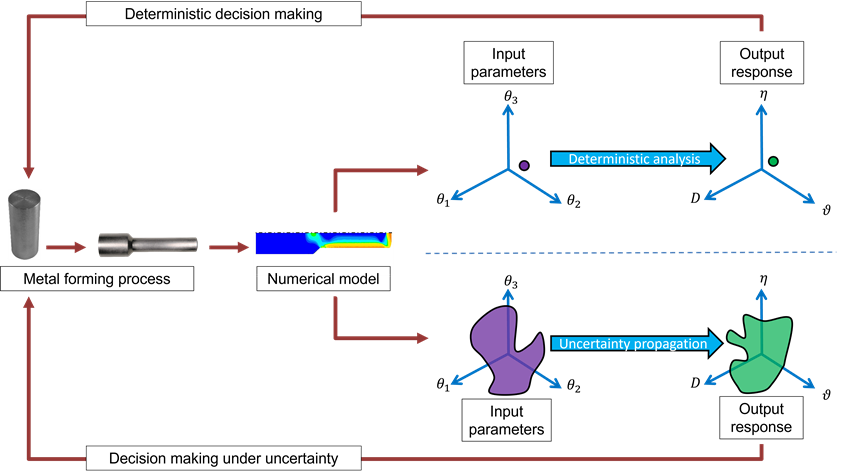
Forming processes induce damage in manufactured metallic components due to their large plastic deformations and stress states. At the same time, quantifying, and controlling this damage formation is of paramount importance to ensure performance of these components during their intended lifetime [Tek17]. To support this, CRC188 developed numerical models to quantify damage a priori. This offers the possibility to make informed manufacturing process decisions, as illustrated schematically in the upper half of Fig. 1. In this figure, θi, i = 1, 2, 3, represent deterministic input parameters of a numerical model characterizing a forming process such as, e.g., material properties, friction, and/or velocity of forming (violet dot). Given those inputs, it is possible to calculate local output responses, such as stress triaxiality η, Lode angle ϑ and damage D. The calculation of such responses entails solving highly complex non-linear finite element analyses. Based on those calculated output responses (green dot in Fig. 1), it is possible to perform decision making, that is, selecting parameters of the forming process (e.g., die design) such that, e.g., damage remains below an acceptable threshold. In practice, it is however difficult to identify precise values for these aforementioned input quantities due to both inherent part-to-part variations as well as potential lack of knowledge on the exact to-be modelled quantities. As a result, one must cope with possible or credible ranges for them. This is represented schematically in the lower half of Fig. 1, where the uncertainty on input parameters is reflected by the violet cloud representing all possible set of values that these parameters may assume. The fact that the parameters governing the forming process become uncertain possesses two major implications, as listed below.
- The output response is no longer characterized by a single, deterministic value. Instead, it is characterized by a set of possible values, as illustrated in the lower half of 1 with a green cloud. Coping with such uncertainties becomes quite challenging, as the decision process on the selection of optimal metal forming parameters, material properties and part design becomes inevitably more involved.
- The characterization of the output response becomes an uncertainty propagation task, since one must compute a set of possible responses. In a traditional sense, propagating uncertainty implies performing repeated deterministic analyses for different values of input parameters. Since a single deterministic analysis can become quite expensive, performing uncertainty propagation may become computationally nearly intractable, even with the recent advances regarding computation power and parallel computing.
The preceding bullet points highlight the necessity of explicitly considering the effects of uncertainty on forming processes for decision making. This task proves to be far from trivial and therefore, has been the subject of active research in the past. The current state of the art regarding uncertainty quantification (UQ) in forming processes and optimal design can be synthesized into three key elements, namely: (1) uncertainty characterization, (2) uncertainty propagation and (3) decision making, which are discussed separately below.
 |
|
Fig. 1: Analysis and design in metal forming: deterministic and uncertain conceptions |
Uncertainty characterization of input parameters
When performing uncertainty characterization, the underlying assumption is that the uncertainties in the forming processes are of random nature. Therefore, they can be characterized through probability distributions. This is an assumption often met in practice in view of the following:
- Raw material usually exhibits variations with respect to nominal values, either regarding its material properties (e.g., Young’s modulus, flow stress) or geometrical dimensions (e.g., thickness)
- Some parameters of a forming process cannot be strictly controlled, e.g., friction in forging processes.
- Other parameters of a forming process can be controlled only up to a certain tolerance. A typical example is geometrical dimensions of a component such as, e.g., a bending angle, due to e.g., spring-back.
The type and parameters of a probability distribution for a particular uncertain parameter can be selected by classical fitting approaches based on data measured experimentally. In particular cases, experimental data allows direct fitting of material properties, as considered in [Jan08] for the case of elastic modulus and yield stress of steel. In some other cases, as documented in [Kre19], a property at the micro-scale is measured (such as, e.g., porosity) and then, its effect at the macro-scale is characterized by considering representative volume elements. It is also possible to infer a certain property indirectly by observing a certain response, as discussed by [Sch22], where it is suggested that records on forces, torques and temperatures may allow identifying material properties. Whenever a property exhibits uncertainty with a spatial component, it is necessary to resort to more sophisticated models, such as random fields, as illustrated in [Fyl09] for modelling sheet metal thickness variations. Note that in [Fyl09] however, the random field reported on was not calibrated considering actual measured thickness data. Concerning indirect uncertainty quantification, i.e., the quantification of parameters that cannot be measured directly, Bayesian updating was illustrated in [Arn17] to identify the hardening modulus and yield stress using numerically simulated springback angles.
Uncertainty propagation
Once the uncertainty affecting the different input parameters of a forming process has been characterized, it becomes necessary to propagate the uncertainty from these inputs to the output responses. This is illustrated schematically in the lower half of Fig. 1. When performing uncertainty propagation, two key points are: (A) how to compute the set of possible responses, i.e., how to perform uncertainty propagation and (B) how to characterize the uncertain response. These two points are discussed in the following.
Approaches for uncertainty propagation
The most straightforward approach for performing uncertainty propagation is resorting to Monte Carlo simulation, as attested in, e.g. [Nar92]. Monte Carlo simulation can be implemented non-intrusively, and it is robust to the dimensionality of the parameter input. The major disadvantage, however, is that it requires a large number of deterministic analyses (up to the order of millions) to provide sufficiently accurate estimates. As a solution hereto, sophisticated propagation schemes, or surrogate models are usually applied. Concerning alternative propagation schemes, linearization has been successfully applied to the reliability analysis of anisotropic metal sheets [Chi13] or reliability analysis of strains in deep drawing forming [Kle04]. Despite being efficient and easy to interpret, the linearization hypothesis is rarely met in realistic forming processes, making the results questionable. Alternatively, importance sampling has been applied [Tan09], which draws samples from a specially designed importance sampling density function. Importance sampling is particularly efficient for addressing low probability events with significant consequences. However, the major disadvantage of importance sampling is that building its associated sampling distribution is usually a challenging task. Concerning surrogate modelling schemes, it is important to ensure that training is carried out appropriately. In this context, the concept of space-filling schemes such as Latin hypercube sampling has been successfully used in forming processes [Leb16]. In practice, different types of surrogate models have been considered for emulating aspects of forming processes, including Gaussian Process Regressions [Str06], polynomial response surfaces [Jan08], Support Vector Machines [Tan09], polynomial chaos expansions [Arn14], and Artificial Neural Networks [Kre19]. Note that no surrogate modelling approach to predict damage, Lode angle or stress triaxiality has been introduced, as well as that all these applied surrogate models provided a mapping to a single scalar value (e.g., springback angle, and local thinning), but not the prediction of field quantities. Further, only Gaussian Process Regression is an exact interpolator and provides an explicit measure of the prediction error.
Characterization of the uncertain response
To describe the variable response, probabilistic descriptors are used that summarize this uncertainty into simple-to-interpret quantities. The simplest probabilistic descriptor are second-order statistics, namely mean and standard deviation, which are particularly useful for ensuring robustness in forming processes, as discussed by [Huo10]. Another probabilistic descriptor of relevance is sensitivity indices, as they reveal how influential an input parameter of a forming process is with respect to a certain response of interest. Local sensitivity analysis quantifies the effect of small variations in the probabilistic description of input parameters over the second-order statistics, as applied in [Pra23]. Global sensitivity analysis aims at apportioning the effect of each uncertain parameter over the outcome of a forming process and can provide valuable insight about forming processes: for example, as illustrated in [Arn14]. In principle, both local and global sensitivity analyses are useful for pinpointing the most influential input parameters. With such information, it is possible to take actions such as, e.g., improving the uncertainty description of a parameter by investing in additional data measurements.
Irrespective of the approach used to propagate uncertainty or the probabilistic descriptor to be considered, it is to be noted that uncertainty propagation necessarily demands performing repeated deterministic analysis. That is, for a number N of realizations of the input parameters, it is necessary to conduct N deterministic analyses to generate a set of N samples of the response. If each of those simulations just takes minutes to converge, uncertainty propagation already becomes extremely demanding. Therefore, one of the central tasks in uncertainty propagation is designing computational schemes that allow decreasing numerical efforts.
Decision making
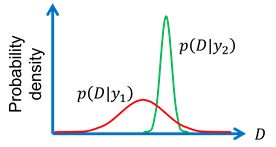
Probabilistic descriptors become most useful when applied as a tool for decision-making to enable the appropriate selection of forming process parameters such as the magnitude of force, speed of forming and the geometry of the component (to name a few). These parameters are denoted with the symbol and are called design variables. The relevance of decision making is that the set of design variables can be selected to ensure that probabilistic descriptors associated with the performance of the component being formed meet specified criteria. To illustrate the latter point, consider the schematic representation in Fig. 2, which shows the probability density function associated with a characteristic damage value at a particular location of a certain metallic component that has been formed considering two different sets of design variables and . As noted from the figure, the forming process produces a component with a mean damage value smaller than that associated with the forming process . Nonetheless, the opposite holds true regarding the standard deviations. In such situation, it may be preferrable to select the forming process . Even though it produces higher average damage, the variability of damage is better controlled, which is a desirable property for ensuring durability across lifetime. The task of selecting a certain set of design variables of a forming process taking into account the effect of uncertainties can be cast as a reliability-based optimization problem (RBO), as discussed by [Wie10]. Indeed, in a RBO problem, the objective function expresses a design criterion (for example, total expected cost) while the constraints ensure manufacturability of the optimal design solution. The main issue with RBO is that it involves a costly double loop problem, where the outer loop corresponds to an optimization problem while the inner loop involves an uncertainty propagation problem. Two solutions are resorting to either surrogate modelling and/or efficient uncertainty propagation schemes, as illustrated in [Mis24]. Also, approaches such as the so-called Sequential Optimization and Reliability Analysis have been applied in metal forming [Sah04].
 |
|
Fig. 2: Probability density associated with damage D for two different designed processes y1 and y2 |
Open Challenges
Significant work has been performed to effectively characterize, propagate and integrate uncertainties in metal forming process decision making. Nonetheless, three open challenges (Ch) pertaining to each separate domain remain to be solved as to unlock the potential of uncertainty quantification methods to optimize metal forming processes in view of controlling damage and its variability.
Ch1. Identification of models for describing uncertainty: Currently, probabilistic models associated with input parameters are calibrated using traditional approaches based on goodness-of-fit. Random field models, while relevant because of the spatial nature of some quantities such as damage distributions, have not been convincingly used based on real data, which is the main challenge. The potential of Bayesian updating has been illustrated, but has not been applied using real experimental datasets, and only on straightforward models with a few parameters have been considered, that on top do not include damage.
Ch2. Strategies for uncertainty propagation: Most of the applied approaches are based on linearization concepts and/or static simulation approaches, which raises questions regarding their performance due to the dimensionality of the input parameter space or nonlinearity of the forming process. Concerning surrogate models, only scalar-valued surrogate models have been deployed, making it impossible to make prediction of field responses such as damage or stress triaxiality. On top of that, the training data for building surrogates of the forming processes is generated statically (offline); often the error of surrogate model is also unknown. Finally, the considered probabilistic descriptors for the considered output quantities are quite classical: second-order statistics, probability of exceedance and sensitivity.
Ch3. Decision making under uncertainty: Most design approaches focus on either geometrical quantities (e.g. thickness, springback angle or wrinkling) or strain measures of the formed metallic component. No methods have been introduced to base the decisions on damage and/or mechanical performance of the produced part. Surrogate models are used in the optimization process but are trained offline, which is not sufficiently efficient for the numerical models of the forming process that include damage prediction.
Challenges Ch1 and Ch3 can, on a meta-level, be rephrased as “how can we best translate state-of-the-art methods from the Uncertainty Quantification (UQ) domain to the field of damage simulation in metal forming, taking into account the immense computational power that is required to run these simulations, and how do these simulations help to control and optimize the damage in these processes?”. Challenge Ch2 on the other hand also poses an interesting question for the UQ community, namely “how can we build effectively accurate surrogate models that are also able to predict quantities that have a spatial distribution over the model geometry”. This makes the problem exciting for both the metal forming as well as for the UQ community, which has potential for synergistic collaboration.
Preliminary Research Work
The Chair for Reliability Engineering (CRE) brings extensive expertise to the CRC188 concerning the characterization, propagation, and decision-making with uncertainty at both scientific and applied levels. Contributions linked to the aforementioned challenges (Ch) include:
Ch1. [Fae19] discusses uncertainty characterization under scarce data, providing a thorough comparison to state-of-the-art Bayesian model updating schemes. Novel Bayesian updating schemes have also been developed recently [Fae23], as well as fundamental understandings on how the physics of a spatially uncertain quantity are linked to the corresponding random field models and their simulation [Fae22].
Ch2. Recent work focussed on surrogate modeling, applying Bayesian approaches for adaptively training Gaussian Process models to predict rare event probabilities [Dan22] and global sensitivity indices [Son22]. The CRE has also developed advanced simulation tools, combining active learning schemes with Line Sampling [Dan23], and using fractional moment approaches for estimating small failure probabilities [Din23].
Ch3. The CRE introduced the operator norm framework, enabling a full decoupling of the double loop associated with reliability-based design optimization. This approach achieves a three-order-of-magnitude gain in computational efficiency for linear models, delivering exact results compared to traditional brute-force double-loop solutions [Fae20].
In the context of damage simulation models developed in TRR188, preliminary work at the CRE assessed the feasibility of reducing numerical costs. This involved exploring surrogate models as alternatives to costly finite element analysis, utilizing Gaussian Process regression and gradient-enhanced Deep Learning. Gaussian Process regression was identified as particularly advantageous due to its active learning strategy, minimizing finite element analyses needed for surrogate training, and allowing control over the precision of estimated probabilistic descriptors. Preliminary results indicate the possibility of performing sensitivity analyses on quantities driving damage with drastic reductions in numerical costs (two to three orders of magnitude) compared to brute force simulation. This provides a promising foundation for the intended research on uncertainty quantification (UQ) in damage simulation for metallic components during forming processes [Böd23]. In terms of Deep Learning, introducing gradient information significantly enhanced training efficiency and prediction accuracy of deep learning models as surrogates for nonlinear finite element models. Gradients were computed using variational methods for gradient analysis developed as part of the C05E project in the first two funding periods. Earlier work by Prof. Faes applied reliability-based design optimization concepts to model the modal behavior of sheet metal-formed cups [Fae18]. The study compared probabilistic reliability-based design optimization with an interval approach to handle limited datasets. Results showed similar outcomes for both approaches, albeit with a considerable computational cost.
As such, preliminary works have been performed covering both the theoretical development of effective and efficient computational schemes to deal with uncertainties, as well as applying these in the specific context of metal forming simulation to also translate these concepts to this practice. This puts the group at the CRE in the best possible position to combine theoretical development of novel approaches to perform UQ with the practical problems that are being faced in the context of predicting damage in metal formed parts.
| [Arn14] | Arnst, M., Ponthot, J.P.: An overview of nonintrusive characterization, propagation, and sensitivity analysis of uncertainties in computational mechanics. International Journal for Uncertainty Quantification, 4 (2014) 59-79. 10.1615/Int.J.UncertaintyQuantification.2014006990 |
| [Arn17] | Arnst, M., Abello Álvarez, B., Ponthot, J.-P., Boman, R.: ‘Itô-SDE MCMC Method for Bayesian Characterization of Errors Associated with Data Limitations in Stochastic Expansion Methods for Uncertainty Quantification’. Journal of Computational Physics 349 (2017) 59–79. 10.1016/j.jcp.2017.08.005 |
| [Chi13] | Chiba, R.: Reliability analysis of forming limits of anisotropic metal sheets with uncertain material properties. Computational materials science 69 (2013)113-120. 10.1016/j.commatsci.2012.11.044 |
| [Dis13] | Dissmann, J. F., Brechmann, E. C., Czado, C., Kurowicka, D.: Selecting and estimating regular vine copulae and application to financial returns. Computational Statistics & Data Analysis 59 (2013) 52-69. 10.1016/j.csda.2012.08.010 |
| [Fyl09] | Fyllingen, Ø., Hopperstad, O.S., Lademo, O.G., Langseth, M.: Estimation of forming limit diagrams by the use of the finite element method and Monte Carlo simulation. Computers & Structures, 87 (2009) 128-139. 10.1016/j.compstruc.2008.07.002 |
| [Guh20] | Guhr, F., Sprave, L., Barthold, F.J., Menzel, A.: Computational shape optimisation for a gradient-enhanced continuum damage model. Computational Mechanics 65 (2020) 1105-1124. 10.1007/s00466-019-01810-3 |
| [Hou10] | Hou, B., Wang, W., Li, S., Lin, Z., Xia, Z.C.: Stochastic analysis and robust optimization for a deck lid inner panel stamping. Materials & Design 31 (2010) 1191-1199. 10.1016/j.matdes.2009.09.033 |
| [Jan08] | Jansson, T., Nilsson, L., Moshfegh, R.: Reliability analysis of a sheet metal forming process using Monte Carlo analysis and metamodels. Journal of materials processing technology 202 (2008) 255-268. 10.1016/j.jmatprotec.2007.09.005. |
| [Kle04] | Kleiber, M., Knabel, J., Rojek, J.: Response surface method for probabilistic assessment of metal forming failures. International journal for numerical methods in engineering 60 (2004) 51-67. 10.1002/nme.954 |
| [Kre19] | Kremer, K., Edler, P., Miska, N., Leichsenring, F., Balzani, D., Freitag, S., Graf, W., Kaliske, M., Meschke, G.: Modeling of structures with polymorphic uncertainties at different length scales. GAMM‐Mitteilungen 42 (2019) 201900006. 10.1002/gamm.201900006 |
| [Leb16] |
Lebon, J., Le Quilliec, G., Breitkopf, P., Filomeno Coelho, R., Villon, P.: Fat Latin Hypercube Sampling and Efficient Sparse Polynomial Chaos Expansion for Uncertainty Propagation on Finite Precision Models: Application to 2D Deep Drawing Process. Computational Methods for Solids and Fluids: Multiscale Analysis, Probability Aspects and Model Reduction (2016) 185-213. 10.1007/978-3-319-27996-1_8 |
| [Mis24] |
Miska, N., Freitag, S., Balzani, D.: Nested Optimal Uncertainty Quantification for an Efficient Incorporation of Random Fields− Application to Sheet Metal Forming. International Journal for Uncertainty Quantification, 14(1) 2024. 10.1615/Int.J.UncertaintyQuantification.2023047256 |
| [Nar92] | Narasimhan, K., Zhou, D., Wagoner, R.H.: Application of the Monte Carlo and finite element methods to predict the scatter band in forming limit strains. Scripta metallurgica et materialia, 26 (1992) 41-46. 10.1016/0956-716X(92)90365-L |
| [Pra23] | Prasad, K., Kumar, D., Krishnaswamy, H., Banerjee, D.K.: Uncertainties in the Swift hardening law parameters and their influence on the flow stress and the hole expansion behavior of dual-phase (DP600) steel specimens. Journal of Materials Engineering and Performance, 32 (2023) 9206-9220. 10.1007/s11665-022-07793-2 |
| [Sah04] | Sahai, A., Schramm, U., Buranathiti, T., Chen, W., Cao, J., Xia, C.Z.: Sequential optimization and reliability assessment method for metal forming processes. In AIP Conference Proceedings 712 (2004) 2009-2013. AIP. 10.1063/1.1766829 |
| [Sch22] | Schowtjak, A., Schulte, R., Clausmeyer, T., Ostwald, R., Tekkaya, A.E., Menzel, A.: ADAPT – A diversely applicable parameter identification tool: Overview and full-field application examples. International Journal of Mechanical Sciences 213 (2022) 106840. 10.1016/j.ijmecsci.2021.106840 |
| [Str06] | Strano, M.: Optimization under uncertainty of sheet-metal-forming processes by the finite element method. Proceedings of the Institution of Mechanical Engineers, Part B: J. of Engineering Manufacture 220 (2006) 1305-1315. 10.1243/09544054JEM480 |
| [Tan09] | Tang, Y., Chen, J.: Robust design of sheet metal forming process based on adaptive importance sampling. Structural and Multidisciplinary Optimization 39 (2009) 531-544. 10.1007/s00158-008-0343-3 |
| [Tek17] | Tekkaya, A.E., Khalifa, N.B., Hering, O., Meya, R., Myslicki, S., Walther, F.: Forming-induced damage and its effects on product properties. CIRP Annals 66 (2017) 281-284. 10.1016/j.cirp.2017.04.113 |
| [Wie10] |
Wiebenga, J.H.: Optimization under uncertainty of metal forming processes-an overview: literature report. Materials Innovation Institute M2i (2010). |
| [Bav23] | Van Bavel, B., Zhao, Y., Faes, M., Vandepitte, D., Moens, D.: ‘Efficient quantification of composite spatial variability: A multiscale framework that captures intercorrelation’. Composite Structures 323 (2023) 117462. 10.1016/j.compstruct.2023.117462 |
| [Fae18*] | Faes, M., Van Doninck, B., Imholz, M., Moens, D.: Product reliability optimization under plate sheet forming process variability. International Workshop on Reliable Engineering Computing (2018). https://lirias.kuleuven.be/retrieve/513809 |
| [Fae19*] | Faes, M., et al.: A multivariate interval approach for inverse uncertainty quantification with limited experimental data. Mechanical Systems and Signal Processing 118 (2019) 534-548. 10.1016/j.ymssp.2018.08.050 |
| [Fae20*] | Faes, M., Valdebenito, M.: Fully decoupled reliability-based design optimization of structural systems subject to uncertain loads. Computer Methods in Applied Mechanics and Engineering 371 (2020) 113313. 10.1016/j.cma.2020.113313 |
| [Fae22*] | Faes, M., Broggi, M., Spanos, PD., Beer, M.: Elucidating appealing features of differentiable auto-correlation functions: A study on the modified exponential kernel. Probabilistic Engineering Mechanics 69 (2022) 103269. 10.1016/j.probengmech.2022.103269 |
| [Dan22*] | Dang, C., Wei, P., Faes, M., Valdebenito, M., Beer, M.: Parallel adaptive Bayesian quadrature for rare event estimation. Reliability Engineering & System Safety 225 (2022). 108621.10.1016/j.ress.2022.108621 |
| [Fae23*] | Faes, M., Klein, N., Pauly, M., Valdebenito, M., Misraji, M.: Approximate Bayesian Computation for Parameter Identification in Computational Mechanics. 14th International Conference on Applications of Statistics and Probability in Civil Engineering, ICASP14 Dublin, Ireland, July 9-13 (2023). http://www.tara.tcd.ie/bitstream/handle/2262/103582/submission_435.pdf |
| [Son22*] |
Song, J., Wei, P., Valdebenito, M., Faes, M., Beer, M.: Data-driven and active learning of variance-based sensitivity indices with Bayesian probabilistic integration. Mechanical Systems and Signal Processing 163 (2022) 108106. 10.1016/j.ymssp.2021.108106 |
| [Dan23*] | Dang, C., Valdebenito, M., Faes, M., Song, J., Wei, P., Beer, M.: Structural reliability analysis by line sampling: A Bayesian active learning treatment. Structural Safety 104 (2023) 102351. 10.1016/j.strusafe.2023.102351 |
| [Din23*] | Ding, C. Dang, C., Valdebenito, M., Faes, M., Broggi, M., Beer, M.: First-passage probability estimation of high-dimensional nonlinear stochastic dynamic systems by a fractional moments-based mixture distribution approach. Mechanical Systems and Signal Processing 185 (2023) 10977. 10.1016/j.ymssp.2022.109775 |
| [Böd23*] | Böddecker, M., Faes, M., Menzel, A., Valdebenito, M.: Effect of uncertainty of material parameters on stress triaxiality and Lode angle in finite elasto-plasticity—A variance-based global sensitivity analysis. Advances in Industrial and Manufacturing Engineering, 7 (2023), 100128. 10.1016/j.aime.2023.100128 |